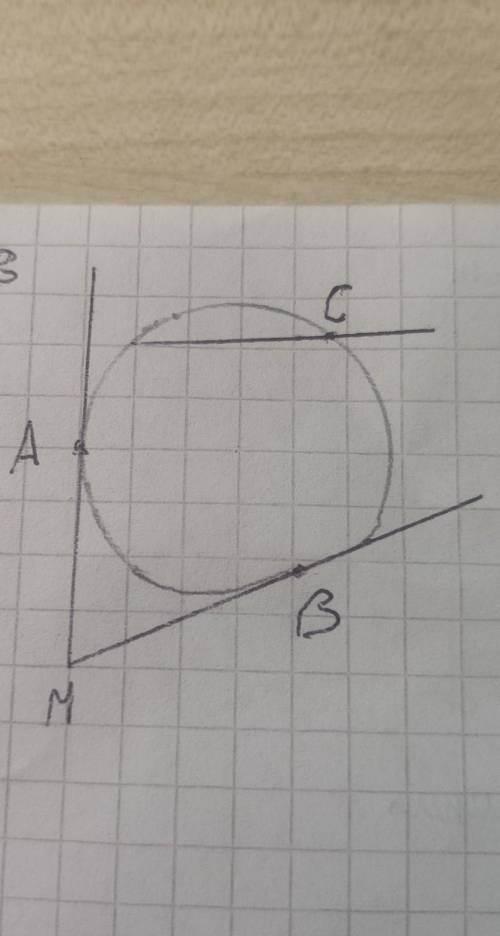
1. все углы по 60. 2.PSD=90, SPD=PDS=45. 3. CAB=50, АВС=60, АСВ=70. 4. BDA=90, DAB=DBA=45
Объяснение:
треугольник MQN
Все стороны равны между собой, значит треугольник равносторонний. Исходя из этого, каждый угол равен 60.
(180:3=60)
треугольник PSD
стороны PS и DS равны между собой, а значит треугольник равнобедренный. Сума всех углов 180 градусов.
180-90=90(угол PSD равен 90)
В равнобедренном треугольнике углы при основе равны.
90:2=45. угол SPD=углу PDS = 45.
треугольник САВ
угол САВ = 180-130=50. (угол МАВ развёрнутый и имеет 180. углы МАС и САВ смежные)
60+50=110. 180-110=70 (угол АСВ)
треугольник BDA
угол ADB = 180-135=45 (угол DAC развёрнутый)
треугольник равнобедренный (стороны BD и AD равны)
углы при основе равны, поэтому угол DBA=BAD=45.
45+45=90, угол BDA 180-90=90
у этих треугольников равны две стороны, общая - медиана, и половинки боковой стороны, на которые медиана делит эту боковую сторону, значит, разнятся только две стороны - другая боковая и основание, у двух этих треугольников, Если боковая сторона АВ=ВС равна х, основание АС=х+3, то х+х+х+3=21, откуда х= тогда периметр АВС равен х+х+3+х+3=21, или 3х=18, х=6,х+3=9, т.е. АВ=ВС=6см, АС=6+3=9, АС=9 см. для этих чисел выполняется неравенство треугольника, т.е. с такими сторонами треугольник существует.
6+9>6; 6+9>6; 6+6>9.
если основание АС=х, то боковая АВ=ВС=х+3, тогда периметр АВС равен х+х+3+х+3=21, откуда х=15/3=5, тогда АС=5см, АВ=ВС=5+3=8/см/ 8+8>5; 5+8=13>8; 5+8=13>8, т.е. задача имеет два решения