7 см, 19 см, 19 см.
Объяснение:
Рассмотрим случай, когда боковая сторона на 12 см больше, чем основание.
Пусть основание равнобедренного треугольника равно х см, тогда каждая из боковых сторон по (х+12) см. Зная, что периметр равен 45 см, составим и решим уравнение:
х + 2•(х+12) = 45
3х + 24 = 45
3х = 45 - 24
3х = 21
х = 21:3
х = 7
7 см - длина основания
7 + 12 = 19 (см) - длина каждой из боковых сторон.
ответ: 7 см, 19 см, 19 см.
Рассмотрим случай, когда боковая сторона на 12 см меньше, чем основание.
Пусть основание равнобедренного треугольника равно х см, тогда каждая из боковых сторон по (х-12) см. Зная, что периметр равен 45 см, составим и решим уравнение:
х + 2•(х-12) = 45
3х - 24 = 45
3х = 45 + 24
3х = 69
х = 69:3
х = 23
23 см - длина основания
23 - 12 = 11 (см) - длина каждой из боковых сторон.
23 см > 11 см + 11 см, нарушено неравенство треугольника, треугольника с такими сторонами не существует.
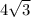 см
см
Объяснение:
Побудуємо прямокутний ΔАВС, з висотою АК=3 см і гострим ∠В=30°.
І варіант рішення:
1) Розглянемо прямокутний ΔКВА.
Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)
Катет ВК=АК/tg(B) ⇒ BK=3√3 (см)
2) Трикутники АВС, КВА та КАС подібні між собою (за гострим кутом як прямокутні трикутники). Тому
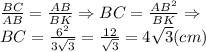
ІІ варіант рішення:
1) Розглянемо прямокутний ΔКВА.
Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)
2) Розглянемо прямокутний ΔКАС.
В ньому ∠С=180°-90°-∠В=60°.
Гіпотенуза АС=АК/sin(С) ⇒ АС=3*2/√3=6/√3 (см)
3) Розглянемо ΔАВС.
Гіпотенуза 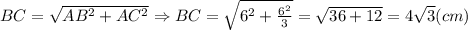
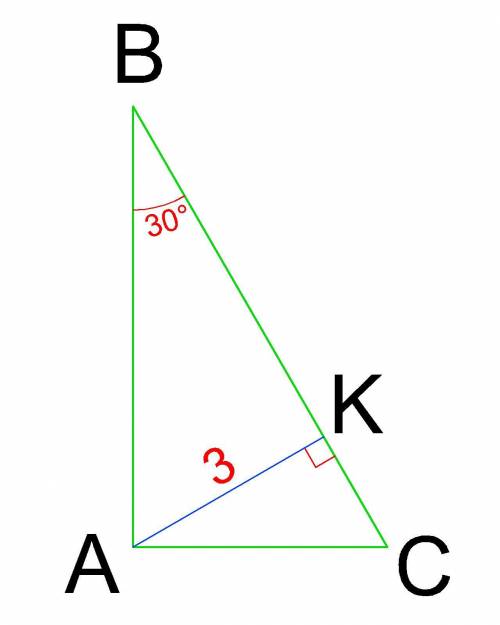
Верные утверждения 1) 4) 5)
Объяснение:
1) В прямоугольном треугольнике высота может совпадать с одной из его сторон - верное утверждение, так как две из трёх высот треугольника совпадают с его катетами
2) Точка пересечения высот произвольного треугольника – центр окружности, описанной около этого треугольника - неверное утверждение, так как центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
4) Высота может лежать и вне треугольника - верное утверждение, так как высоты тупоугольного треугольника, проведённые из вершин острых углов, опускаются на продолжения сторон, образующих тупой угол.
5) Треугольник со сторонами 6,8,10 - прямоугольный - верное утверждение, так как для сторон этого треугольника выполняется теорема Пифагора: 10² = 6² + 8² ⇒ 100 = 36 + 64 ⇒ 100 ≡ 100
6) Существует треугольник со сторонами 6, 8, 15 - неверное утверждение, так как в этом случае не выполняется неравенство треугольника: длина любой стороны треугольника всегда меньше суммы длин двух его других сторон, а в данном утверждении 6+8<15