случае наименьший угол равен ∠ =
180
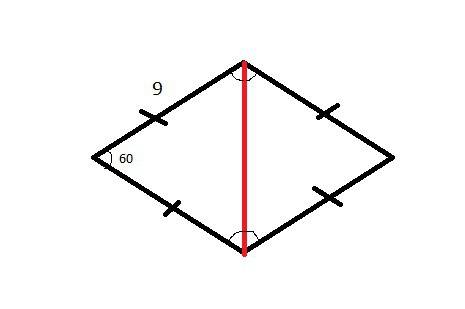
Объяснение:Рассмотрим треугольник ABC с углами ∠ = ∠ = , ∠ = 180 − 2. Чтобы
получилось два треугольника прямая должна проходить через одну из вершин.
Рассмотрим случай, когда она проходит через вершину A и делит треугольник на два: ADB
и ADC (см. рис.).
Треугольник ADC является равнобедренным в двух случаях:
I) ∠ = . Приравнивая ∠ = ∠ (т.к. угол ∠ тупой) приходим к
уравнению 180 − 2 = 3 − 180
, откуда = 72
. Наименьший угол тогда
равен ∠ = 36
II) ∠ = ∠ =
180−
2
. Тогда 3
2
− 90 = 180 − 2, откуда =
540
7
С
А Н В
треугольник АВС равнобедренный (АС=ВС), значит углы при основании равны.
уголС=120градусов
уголА=уголВ=(180-120):2=30градусов
Катет, лежащий против угла 30 градусов равен половине гипотенузы, значит СН=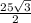
По св-вам равнобедренного треугольника, высота является и медианой => АН=НВ
АН^2=(25корней из3)^2-(25корней из3 /2)^2
АН^2=1875-468,75=1406,25
АН=37,5
АВ=37,5*2=75см.