Дело в том, что в трапеции получаются два подобных прямоугольных треугольника: koc, aom.
Дальше по отношениям: ao/oc = ko/om = kc/am
подставляем в последнее отношение известные данные, тем самым находим коэффициент - 3.
Значит, ос меньше ао в три раза, т.е. он 2,5 дм.
по теореме пифагора находим ко = 0,5 корень из 5.
ом больше ко в три раза: 1,5 корень из 5
И складываем ом+ко.= 2 корень из 5
Задача: Знайти радіус кола, вписаного в рівносторонній трикутник, якщо радіус кола, описаного навколо цього трикутника, дорівнює 16 см.
Рішення:
Формула кола, вписаного в рівносторонній трикутник:
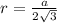 , де а — сторона правильного тр-ка
, де а — сторона правильного тр-ка
Знайдемо сторону а через формула кола, описаного навколо рівностороннього тр-ка:
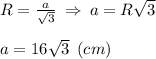
Підставимо значення у формулу кола, вписаного в рівносторонній тр-к

Відповідь: Радіус кола, вписаного в рівносторонній трикутник, рівний 8 см.
Задача: Точка перетину висот BK і PH трикутника BEP є центром вписаного в нього кола. Доведіть, що тр-к BEP рівносторонній.
Рішення:
Центром вписаного в коло трикутника є перетин бісектриса тр-ка, отже і BK та PH є бісектрисами. Висота є бісектрисою, якщо суміжні сторони рівні.
BK — висота/бісектриса ⇒ PB = EB;
PH — висота/бісектриса ⇒ PB = EP.
Відповідно, PB = EB = EP ⇒ ΔBEP — рівносторонній, що і потрібно було довести.
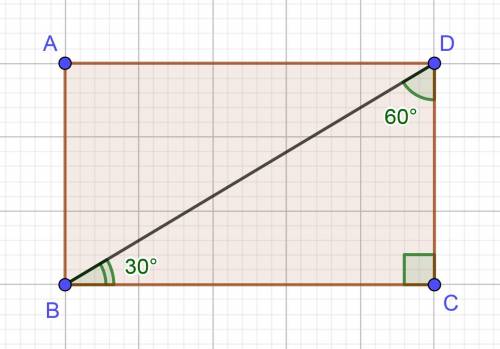
Нехай дано прямокутник ABCD, BD — діагональ, DC = 10 см, ∠BDC = 60°.
Р-мо BDC:
∠BCD = 90° — як кут прямокутника, отже ΔBDC — прямий, ∠BDC = 60° — за умовою, тоді ∠DBC за теоремою про суму кутів трикутника буде дорівнювати:
∠DBC = 180°−90°−60° = 30°.
По властивості катета, який лежить напроти кута 30°, гіпотенуза трикутника буде рівна:
BD = 2*DC = 2*10 = 20 (cm)
Знайдемо інший катет за т. Піфагора:
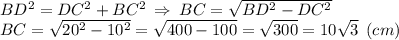
Підставимо значення у формулу площі прямокутника:

Відповідь: Площа прямокутника рівна 100√3 см² або приблизно 173,2 см².
ОМ = корень (АО в квадрате - АМ в квадрате) = корень (56,25-36)=4,5
Треугольники АОМ и КОС подобные как прямоугольные по остому углу.
АМ/ОМ=КС/КО
6/4,5=2/КО
КО=(4,5 х 2) / 6 = 1,5
КМ= 4,5+1,5=6