осевое сечение цилиндра - это прямоугольник. Нам известна площадь осевого сечения - 12 см в квадрате. Площадь прямоугольника = а*в(стороны прямоугольника)=12, высота цилиндра, которая равна 2 - это и есть в - сторона прямоугольника.
Получается, что Sпрямоугольника=а*2=12
Отсюда, а=12/2=6
а-это сторона прямоугольника и диаметр нашего основания, круга.
Формула круга = пR^2
Найдем радиус: диаметр/2=6/2=3
Подставляем: п*3^2=9п
ответ : 9п
Условие задачи неполное. Должно быть так:
Основанием тетраэдра МАBC служит треугольник АBC в котором AB = BC и АС = 2а√3. Точка О принадлежит АС отрезок МО перпендикулярен АС и ОА = ОС. Расстояние от точки О до прямой МB равно а. Найти угол между плоскостями (AMB) и (CMB).
Проведем ОК⊥МВ. Тогда ОК - расстояние от точки О до прямой МК и ОК = а.
ΔАВС равнобедренный, значит медиана ВО (ОА = ОС по условию) является и высотой,
ВО⊥АС,
МО⊥АС по условию, значит
АС⊥(МОВ).
МВ лежит в плоскости (МОВ), значит МВ⊥АС и ОК⊥МВ по построению, тогда МВ⊥(АКС) и значит ∠АКС - линейный угол двугранного угла между плоскостями (АМВ) и (СМВ).
АО = ОС = АС/2 = а√3, МО - медиана и высота в треугольнике МАС, значит он равнобедренный,
МА = МС.
ΔМАК = ΔМСК по гипотенузе и катету (∠АКМ = ∠СКМ = 90°, МА = МС и МК - общий катет), тогда
АК = КС, значит медиана ОК в равнобедренном треугольнике АКС является и высотой и биссектрисой, т.е. ОК⊥АС и ∠АКС = 2∠ОКС.
ΔОКС: ∠КОС = 90°,
tg∠OKC = OC / OK = a√3 / a = √3
Тогда ∠ОКС = 60°.
∠АКС = 2∠ОКС = 120°
осевоге сечение цилиндра- прямоугольник с высотой 2 см, тогда
Основание прямоугольника (оно же и диаметр основания) = 12/2=6см
Тогда радиус основания=6/2=3см
Площадь основания=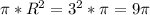
или 9*3,14=28,26 см2