\begin{gathered} 3\cos 2x = 7\cos x \\ 3(2\cos ^{2}x - 1) - 7\cos x = 0 \\ 6\cos ^{2}x - 3 - 7\cos x = 0 \\ \cos x = t \\ 6t^{2}-7t-3=0 \\ D = 49 + 24*3 = 121 \\ \\ t_{1} = \dfrac{7 + 11}{12} = 1.5 \ ; \ \ \ t_{2} = \dfrac{7-11}{12} = -\dfrac{1}{3} \\ \\ $\left[ < br / > \begin{gathered} < br / > \cos x = 1.5 \\ \cos x = -\dfrac{1}{3} \\ < br / > \end{gathered} < br / > \right.$ \ \ \ ; \ < br / > $\left[ < br / > \begin{gathered} < br / > x \notin [-1;1] \\ x = \pm \arccos( -\dfrac{1}{3}) + 2\pi n, n \in Z < br / > \end{gathered} < br / > \right.$ \end{gathered}
Дано:
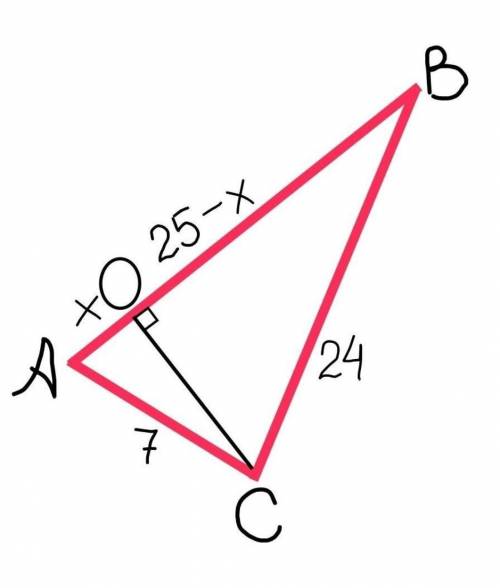
АС=7 см;
АВ=25 см;
ВС=24 см.
СО – высота, проведенная к АВ.
Высота, пересекаясь со стороной, к которой проведена, образует прямой угол.
То есть угол ВОС=90° и угол АОС=90°.
Следовательно ∆ВОС – прямоугольный с прямым углом ВОС и ∆АОС – прямоугольный с прямым углом АОС.
Пусть АО=х, тогда ВО=АВ–АО=25–х.
По теореме Пифагора в прямоугольном треугольнике ВОС:
ВС²=ВО²+СО²
СО²=ВС²–ВО²
СО²=24²–(25–х)²
СО²=576–625+50х–х²)
СО²=–х²+50х–49 (Ур 2)
По теореме Пифагора в прямоугольном треугольнике АОС:
АС²=АО²+СО²
СО²=АС²–АО²
СО²=7²–х²
СО²=49–х² (Ур 2)
Тогда можем составить уравнение, объединив Ур 1 и Ур 2, получим:
–х²+50х–49=49–х²
50х=98
х=1,96
Тоесть АО=1,96 см.
Подставим значение АО и известное значение АС в уравнение СО²=АС²–АО², получим:
СО²=49–3,8416
СО²=45,1584
СО=6,72 см.
ответ: 6,72 см.
В правильной шестиугольной призме АBCDEFFA₁B₁C₁D₁E₁F₁ все ребра которой равны 1, найдите расстояние от точки В до прямой С₁F
(Правильная призма — это прямая призма, основанием которой является правильный многоугольник.)
-----------
Объяснение подробное и поэтому длинное, хотя решение задачи довольно простое.
Расстояние от точки до прямой - длина отрезка, проведенного от точки перпендикулярно к этой прямой
Соединим попарно точки C₁ и F, B и C₁, B и F.
Если провести через середины ВС и ЕF прямую, то она - диаметр вписанной в основание окружности. ВF параллельна этому диаметру и перпендикулярна СВ.
СВ, проекция наклонной С₁В, перпендикулярна ВF ⇒
по т. о трех перпендикулярах С₁В ⊥BF ⇒
⊿ ВС₁F прямоугольный с прямым углом C₁BF
Искомое расстояние - высота ВН, проведенная из прямого угла этого треугольника к гипотенузе C₁F
C₁F найдем из ∆ С₁BF- он прямоугольный, т.к. все ребра правильной призмы перпендикулярны основанию.
СF равен длине двух сторон основания, т.е. 2.
СС1=1 по условию.
С₁F=√(2²+1²)=√5
C₁B=√(CC₁²+CB²)=√2
BF можно найти по т.косинусов, можно из прямоугольного ∆АВМ, в котором угол АВМ=30º ( как угол при основании равнобедренного ∆ ВАF, где угол при А=120, а угол МАВ=60º).
ВМ =АВ*sin60º=√3):2
BF=2 BM=√3
S ∆ BC₁F=BC₁•BF:2=(√2•√3):2=(√6):2
ВН ∆ BC₁F=2S:C₁F=(√6):√5 или, если извлечь корни, примерно 1,095 (ед. длины)