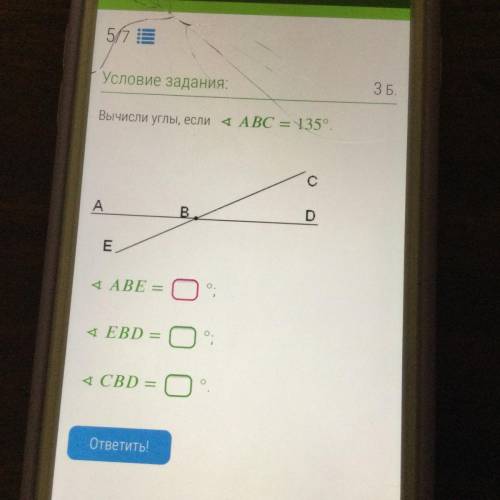
∠ABE = 45°
∠EBD = 135°
∠CBD = 45°
Объяснение:
∠ABC = ∠EBD, ∠ABC + ∠EBD = 135° + 135° = 270°
360° - 270° = 90° - углы ABE и ∠CBD вместе
90° : 2 = 45° - ∠ABE/
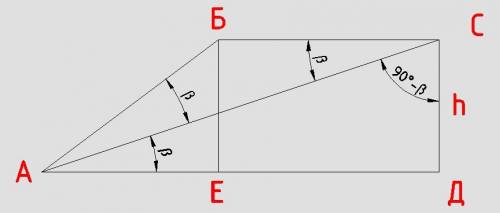
Даны координаты вершин треугольника: А(х1; у1), В(х2; у2), С(х3; у3).
AM, BM – медианы треугольника, О – точка пересечения медиан.
Так как М – середина ВС, то её координаты: М(х2 + х3)/2; (у2 + у3)/2).
Находим координаты вектора АМ.
АМ = (((х2 + х3)/2) – х1; ((у2 + у3)/2)) – у1).
АМ = (((х2 + х3 – 2х1)/2); ((у2 + у3 – 2у1)/2)).
Далее используем свойство, что медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то есть АО = 2*ОМ.
Тогда АО = (2/3) АМ.
Значит, координаты вектора АО равны:
АО = ((2/3)*((х2 + х3 – 2х1)/2); (2/3)*((у2 + у3 – 2у1)/2)).
АО = (((х2 + х3 – 2х1)/3); (((у2 + у3 – 2у1)/3)). (1)
Обозначим координаты точки О(хо; уо).
Выведем вектор АО через координаты точек А и О:
АО = ((хо – х1); (уо – у1)). (2)
Приравняем в выражениях (1) и (2) координаты точки О.
((хо – х1) = ((х2 + х3 – 2х1)/3),
(уо – у1) = ((у2 + у3 – 2у1)/3).
Отсюда получаем искомое выражение для определения координат точки пересечения медиан:
хо = ((х1 + х2 +х3)/3),
уо = ((у1 + у2 + у3)/3).
∠ABE = 45°
∠EBD = 135°
∠CBD = 45°
Обьяснение:
∠ABE = ∠CBD; ∠ABC = ∠EBD как вертикальные,
∠CBD = AD - ∠ABC= 180° - 135° = 45°
Так что ∠ABE=∠CBD = 45°; ∠ABC = ∠EBD=135°