ответ первого пользователя верный. Но так как он очень лаконичный, даю более подробное решение.
Хорда, стягивающая дугу, на которую опирается центральный угол, является
основанием равнобедренного треугольника с боковыми сторонами - радиусами, и углом при вершине О, равным 60°.
Поэтому два других угла также равны 60°, и потому треугольник АОВ - не просто равнобедренный, а равносторонний.
Следовательно, хорда АВ равна боковым сторонам этого треугольника и равна радиусу окружности.
Радиус по условию задачи равен 7.
АВ=7.
Итак, DA1B1C1 совпадает с DA1B2C2, значит, DA1B1C1= DA1B2C2=DABC.
DA1B1C1=DABC
Теорема доказана.
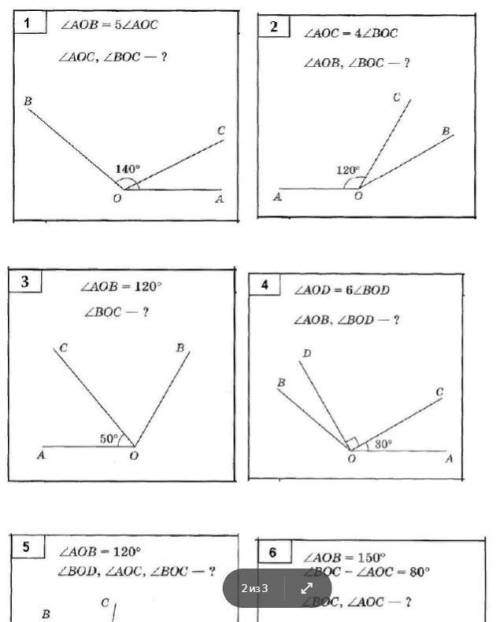
1) AOB x, тогда AOC - 5x. 140 = 5x x = 28
AOC = 28, BOC = 112
2) пусть COB = x, тогда AOC 4x, значит AOC = 30
AOB = 150; BOC = 30
3) если AOB = 120, а AOC = 50, то BOC= 120-50 = 70
4) AOD = AOC + DOC = 30 + 90,т.к DOC прямой угол.
AOD = 120 , BOD = 120:6 = 20
AOB =BOD + AOD = 120+20 = 140
Объяснение:
остальное не видно, извини