Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P и образуют два равных треугольника KPN и MPL. Расстояние между точками K и L равно 36,7 см. Какое расстояние между точками M и N?
1. У равных треугольников все соответствующие элементы равны, стороны KP =
и NP =
как соответствующие стороны равных треугольников.
∡
=
° и ∡
=
°, так как их смежные углы ∡ KPN = ∡ MPL =
°.
По первому признаку треугольник KPL равен треугольнику
.
2. В равных треугольниках соответствующие стороны равны. Для стороны KL соответствующая сторона — MN.
MN =
см.
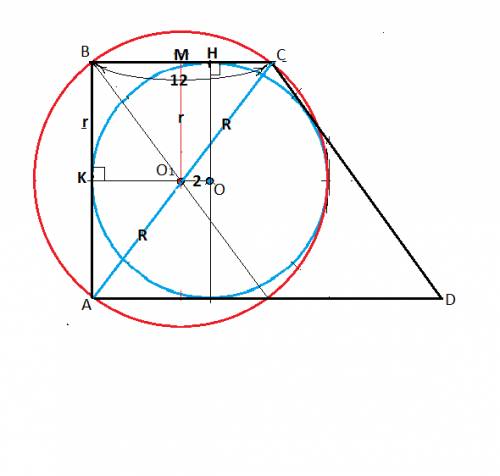
Угол АСD=90
Угол D=60
Всего в треугольнике 180 градусов ⇒ Угол САD=180-90-60=30
Угол САВ тоже равен 30, потому что АС - биссектриса. Всего угол А=60.
А=D=60 ⇒ трапеция АВСD - равнобедренная.
Рассмотрим ΔАСD
Он - прямоугольный. Угол А в нём равен 30 градусов ⇒ СD = 1/2AD ⇒ AD=2CD
Углы в трапеции D и С - односторонние ⇒ C+D=180
D=60 ⇒ C=120. Угол АСD=120-90=30
И угол ВАС=30 ⇒ ΔАВС - равнобедренный ⇒ АВ=ВС
Пусть CD=АВ=х. P=35, тогда
х+х+х+2х=35
5х=35
х=35/5
х=7.
х=АВ=7
Задача решена.
ответ: АВ=7