2/3 3/4 5/3 5/7 :) Правильно должно быть
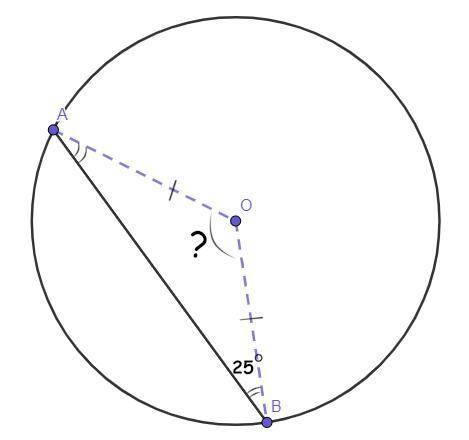
АВ хорда окружности с центром в точке О. Найдите угол АОВ, если угол АВО = 25°.
- - -
Дано :Окружность.
Точка О - центр данной окружности.
Отрезок АВ - хорда окружности.
∠АВО = 25°.
Найти :∠АОВ = ?
Решение :Рассмотрим ΔАВО.
Отрезки АО = ВО (так радиусы одной окружности), следовательно, ΔАВО - равнобедренный (по определению).
У равнобедренного треугольника углы у основания равны.Основание ΔАВО - отрезок АВ (так как АО и ВО - боковые стороны).
Тогда -
∠АВО = ∠ОАВ = 25°.
Сумма внутренних углов треугольника равна 180°.То есть -
∠АВО + ∠ОАВ + ∠АОВ = 180°
∠АОВ = 180° - ∠АВО - ∠ОАВ
∠АОВ = 180° - 25° - 25°
∠АОВ = 130°.
ответ :130°.
любое число в нулевой степени равно единице, поэтому (16,017)^0 = 1
(1/5)^-3 = 125, потому что 5^3 = 125, а при отрицательной степени число переворачивается( (1/5)^-1 -> 5 )
чтобы возвести 16 в степень 3/4 можно представить 16 как 2 в 4 степени, тогда получается, что в таком виде, как (2^4)^3/4, степени сократятся, потому что при возведении числа в степени в ещё одну степень, эти степени перемножаются между собой, отсюда получается (2^4)^3/4 = 2^(4*3/4) = 2^3 = 8
тогда выражение приобретает вид: 1 - 125 + 5*8 = 1 - 125 + 40 = -84
Объяснение:
14/21=2/3
18/24=3/4
25/15=5/3=1 2/3
25/35=5/7