построем рисунок, в треугольнике ВСD: ВС=СD (т.к. шестиугольник правильный), угол равен 120 градусов, (по формуле для нахлждения угла в правильном многоугольнике а=180(n-2)/n), проведһм перпендикуляр СН, угол ВHC = (180-120)/2=30 (т.к. треугольник равнобедренный, углы при основании равны) следовательно, СН=0,5ВС = корень из 48 по полам=корень из двенадцати (после преобразования)
теперь ВН = (по теореме пифагора) корень из (48-12) = корень из 36 = 6
ВН равно HD (т.к. в равнобедренном треугольнике высота равна медиане) следовательно ВD=2BH = 6*2 = 12
Как то так!
Объяснение:
Найдем угол А: 90 - 27 = 63 градуса(сумма острых углов в прямоугольном треугольнике равна 90 градусов).
Найдем гипотенузу AB.
Синус угла A равен отношению противолежащего данному углу катета BC к гипотенузе AB.
Иначе говоря:
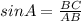
Синус 63 градусов равен 0,891007.
Выразим из этой формулы AB:
AB = BC/sinA = 13/0,891007 = 14,6
Для того, чтобы найти катет AC, мы должны использовать тангенс, т.к. именно эта тригонометрическая функция связывает оба катета.

Тангенс - это отношение противолежащего катета к прилежащему.
Тангенс 27 градусов равен 0,21.
Чтобы найти AC, мы тангенс угла B умножим на BC.
AC = tgB * BC = 0,51 * 13 = 6,63
С= 2пr
C= 2п*12=24п
п 3,14
3,14
С 75,36
75,36