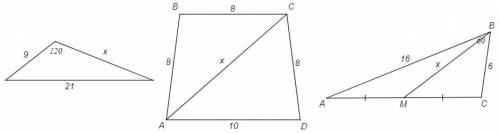
5)
21^2 =9^2 +x^2 -2*9*x*cos120 =>
x^2 +9x -360 =0 =>
x = -9 +√(81 +4*360) /2 =(39-9)/2 =15 (см) (x>0)
7)
теорема косинусов для △ABC и △ADC
∠B =180-∠D => cosB = -cosD
x^2 =8^2 +8^2 -2*8*8*cosB
x^2 =8^2 +10^2 -2*8*10*cosD
(x^2 -128)/(x^2 -164) = -4/5 =>
5x^2 -640 = -4x^2 +656 =>
x^2 =1296/9 => x=12 (см)
8)
AC^2 = 16^2 +6^2 -2*16*6*cos60 => AC=14
AM=MC=7
теорема косинусов для △AMB и △BMC
∠AMB =180-∠BMC => cosAMB = -cosBMC
16^2 =x^2 +7^2 -2*x*7*cosAMB
6^2 =x^2 +7^2 -2*x*7*cosBMC
(x^2 -207)/(x^2 +13) = -1 =>
2x^2 =194 => x=√97 (см)
1. В системе координат нарисуй треугольник ABC с координатами вершин:
A(−1;−1), B(−4,2;−1), C(−1;−4,2);
2. Нарисуй треугольник A1B1C1, полученный при повороте треугольника ABC вокруг начала координат на 180°.
3. Нарисуй треугольник A2B2C2, полученный в симметрии треугольника A1B1C1 относительно прямой x=0.
Определи координаты:
image
image
image
Каким образом можно было из треуголника ABC сразу получить треугольник A2B2C2?
центральной симметрией относительно начала координат
параллельным переносом на вектор (1;1)
симметрией относительно прямой y=0
симметрией относительно оси Ox
поворотом на 180 градусов вокруг начала координат
Объяснение:
Д
С М Е
т.к. уголДМС острый, значит уголДМЕ тупой, т.к. они смежные и их сумма =180гр.
Рассмотрим треугольникМДЕ:
у него уголДМЕ тупой, значит ДЕ - большая сторона этого треугольника, т.к. против большего угла лежит большая сторона.
в треугольнике не может быть два тупых угла, т.к. сумма всех углов треугольника 180 градусов. Значит, ДЕ - единственная большая сторона этого треугольника, значит ДЕ>ДМ.