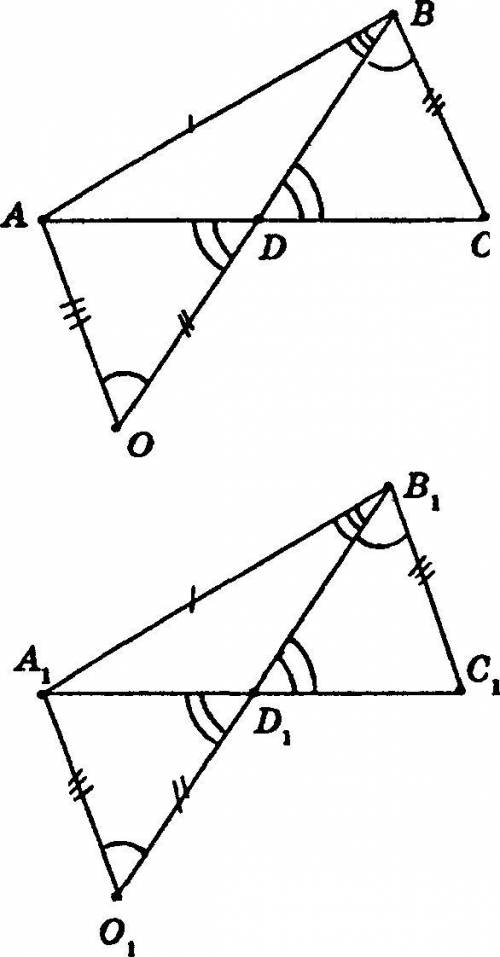
Продлим медианы так, чтобы: BD = DO, B1D1 = D1O1. В ΔADO и ΔDBC: AD = DC (из условия) BD = DO (по построению) ∠ADO = ∠BDC (как вертикальные).
Таким образом, ΔADO = ΔBDC по 1-му признаку равенства треугольников; откуда АО = ВС как лежащие в равных треугольниках против равных углов, ∠AOD = ∠DBC.
Аналогично ΔA1D1O1 = ΔD1B1O1 и А1О1 = В1С1, ∠A1O1D1 = ∠D1В1С1.
Т.к. ВС = В1С1, то АО = А1О1. В ΔАОВ и ΔА1О1В1: АВ = А1В1 (из условия), АО = А1О1 (по построению), ВО = В1О1 (по построению),
Таким образом, ΔАВО = ΔА1В1О1 по 3-му признаку равенства треугольников. Откуда
∠A1B1C1 = ∠A1B1D1 + ∠D1B1C1, т.к. правые части равны, то и левые должны быть равны.
Следовательно ∠АВС = ∠А1В1С1.
В ΔABC и ΔA1В1С1:
∠АВС = ∠А1В1С1, АВ = А1В1, ВС = В1С1 (из условия).
Таким образом, ΔАВС = ΔА1В1С1 по 1-му признаку равенства треугольников, что и требовалось доказать.
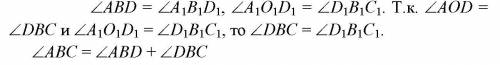
1) Пусть точка C - точка пересечения отрезков AB и MK.
Тогда по первому признаку равенства треугольников (две стороны и угол между ними) будут равными треугольники AKC и CBM.
А значит и углы тругольников AKС и СMB равны. Из этого следует, по теореме о параллельных прямых, так как накрест-лежащие углы (AKС и СMB) равны, то отрезки AK и MB параллельны.
2) См. рисунок.
Так как CH- биссектриса, то углы KCH и HCT равны между собой и равны половине угла KCP, т.е. 29°.
Так как CK и TH параллельны, то накрест-лежащие углы KCH и CHT равны, также 29°.
Угол CTH = 180 - HCT - CHT =180-29-29=122°.
Таким образом углы в треугольнике CHT: 29, 29, 122.