Равносторонних трапеций не бывает, скорее всего имеется в виду равнобокая трапеция (с равными боковыми сторонами).
Если одну из диагоналей перенести в общую вершину со второй диагональю, то получим равнобедренный прямоугольный треугольник с прямым углом вверху и углами по 45 градусов у нижнего основания.
Тогда легко находится высота треугольника - она и высота трапеции.
Высота равна половине гипотенузы нового треугольника, которая равна 16 + 20 = 36 см.
ответ: длина высоты трапеции равна 36/2 = 18 см.
Рисунок прилагается. Таких внешних касательных существует всего две. Они пересекаются в точке G. BD и CF - радиусы, перпендикулярные касательной GE. Треугольники GDB и GFC подобны по двум углам (G - общий угол, а также ∠GBD=∠GFC=90° (как раз эти самые радиусы)
Тогда из подобия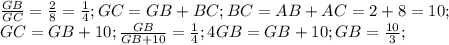
Наше искомое расстояние AP. Это заодно значит, что AP перпендикулярно GT (второй касательной, можно было так же начертить и с первой, это не принципиально). Тогда треугольники GBH и GAP тоже подобны по двум углам (G - общий и ∠GHB=∠GPA=90°)
и значит, что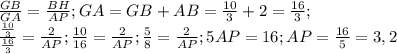
ответ: 3,2 см.