СПОЧНО ДАЮ 25 БЫЛЛОВ На луче с началом в точке А отмечены точки В и C. Известно, что AB = 10,4см ВС в четыре раза меньше AB. Какую длину может иметь отрезок АС,если точка В лежит между точек АС?

👇

Увидеть ответ

Ответ:

kirillarhipenc1

12.04.2020

AC = 13см

Объяснение:

тк АВ 10, 4, а ВС в 4 раза меньше, то получим следующий пример:

10,4:4 = 2,6

АВ+ВС=АС

10,4 + 2,6 = 13

4,7(59 оценок)

Открыть все ответы

Ответ:

pashamironov20

12.04.2020

В треугольнике ABC, AB = BC. Медианы треугольника пересекаются в точке O, OA = 5, OB = 6. Найдите площадь треугольника ABC.

============================================================

точка О - точка пересечения медиан ( см приложение )По свойству пересечения медиан в ΔАВС ВО:ОЕ = 2 : 1⇒ ОЕ = ВО/2 = 6/2 = 3 По свойству равнобедренного треугольника ВЕ⊥АС, ВЕ - медиана, высота, биссектрисаВ ΔАОЕ: по теореме ПифагораАЕ² = АО² - ОЕ² = 5² - 3² = 25 - 9 = 16АЕ = 4АС = 2•АE = 2•4 = 8Значит, S abc = BE•AC/2 = 9•8/2 = 36ОТВЕТ: S abc = 36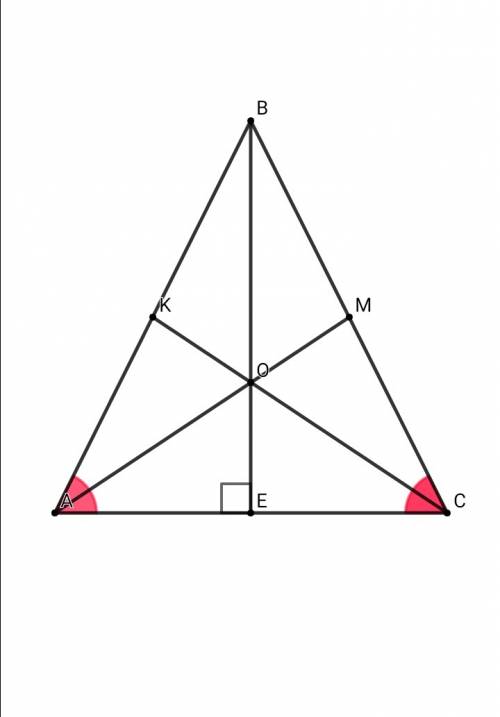
Втреугольнике abc,ab=bc.медианы треугольника пересекаются в точке o,oa=5 ob=6.найдите площадь треуго

Втреугольнике abc,ab=bc.медианы треугольника пересекаются в точке o,oa=5 ob=6.найдите площадь треуго

4,4(51 оценок)

Ответ:

Filka7

12.04.2020

БИЛЕТ №19. 1.На листочке бумаги чертишь по линейке одну сторону. Обозначь, например конечные точки А и ВЦиркулем на линейке берешь размер второй стороны, в точку А ставишь иголочку циркуля. Карандашом циркуля проводишь дугу.Теперь берешь циркулем размер третьей стороны. Из точки В проводишь циркулем дугу. Где дуги пересеклись, поставь точку С. Это третья вершина твоего треугольника. Соедини точки А, В, С по линейке.А теперь подумай -если сумма длин сторон АС и ВС будет меньше или равна длине стороны АВ, разве твои дуги пересекутся? Попробуй для интереса. Нет, не пересекутся.Отсюда и делаем вывод ( для этого и задачу задали) -сумма двух сторон должна быть больше третьей стороны.
2.Теорема (Соотношение между сторонами и углами треугольника) . В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что угол С больше угла В. Для этого отложим на луче АВ отрезокAD, равный стороне АС. Треугольник АСD - равнобедренный. Следовательно, Ð1 = Ð2. Угол 1 составляет часть угла С. Поэтому Ð1 < ÐC. С другой стороны, угол 2 является внешним углом треугольника ВСD. Поэтому Ð2 > ÐB. Следовательно, имеем ÐC > Ð1 = Ð2 > ÐB. Следствие: В произвольном треугольнике против большего угла лежит большая сторона. Докажем, что если в треугольнике АВС угол С больше угла В, то и сторона АВ больше стороны АС. Действительно, эти стороны не могут быть равны, так как в этом случае треугольник АВС был бы равнобедренным и, следовательно, угол С равнялся бы углу В. Сторона АВ не может быть меньше стороны АС, так как в этом случае, по доказанному, угол С был бы меньше угла В. Остается только, что сторона АВ больше стороны АС.
3.1) 2+3=5(см) - боковая сторона. 2) 5+2=7(см) - основание Проверка: 5х2=10, 10-3=7 Так же: х - основание у - боковая сторона у+2=х х+3=у2 у+2+3=у2 Так как чтобы из у получить у2 надо к у прибавить у, то (2+3)=у БИЛЕТ №201. Поставить острие циркуля в вершину угла и на обоих лучах угла отложить равные отрезки (сделать засечки). Не меняя раствора циркуля поставить поочередно острие циркуля на засечки, сделанные в шаге 1, и провести дуги, так, чтобы они пересеклись. Точку пересечения дуг соединить с вершиной угла. Это и будет биссектриса.
2.Пусть Δ ABC – равнобедренный с основанием AB , и CD – медиана, проведенная к основанию. В треугольниках CAD и CBD углы CAD и CBD равны, как углы при основании равнобедренного треугольника (по теореме 4.3), стороны AC и BC равны по определению равнобедренного треугольника, стороны AD и BD равны, потому что D – середина отрезка AB . Отсюда получаем, что Δ ACD = Δ BCD .Из равенства треугольников следует равенство соответствующих углов: ACD = BCD , ADC = BDC . Из первого равенства следует, что CD – биссектриса. Углы ADC и BDC смежные, и в силу второго равенства они прямые, поэтому CD – высота треугольника.Теорема доказана.
3.Если внешний угол А равен 120 => сам угол А = 60 (как смежные углы, т. е. 180-120). если угол А = 60 => угол В = 30 градусов. В прямоугольном треукгольнике напроитв угла в 30 градусов лежит катет равный половине гипотенузы. то есть. АВ = 2 * АС. =>2*АС + АС = 18.=> 3*АС = 18 => АС = 6 => АВ = 18 - 6 = 12БИЛЕТ №211.Возьми циркуль и выстави на нём длину чуть меньше отрезка. Иглу на начало отрезка, чертим окружность. Иглу на конец отрезка, чертим окружность. Окружности пересекутся в двух точках, соедини эти точки прямой. Прямая пересечёт середину заданного отрезка.
2.Пусть при пересечении прямых а и b секущей c сумма односторонних углов равна 180. Т. к. эти углы 3 и 4 смежные, то 3+4=180. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые параллельны.
3.AO=MH, так как ОС и ЕН - медианы треугольников ABC и MKE. Так как углы С и Е равны и ВС=КЕ, то углы АСО и МЕН также равны. Так как углы В и К равны, то соответственно углы А и М равны, из этого следует, что треугольники АСО и МЕН равны по стороне и двум прилежащим к ней углам.

4,7(1 оценок)

Это интересно:

Транспорт

28.04.2020

Как заменить ручки на руле мотоцикла: подробное руководство...

Семейная-жизнь

18.02.2023

Как придумать крутое и запоминающееся прозвище для себя или других?...

Образование-и-коммуникации

26.01.2022

Как хорошо учиться: советы, методы и секреты...

Компьютеры-и-электроника