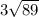
Объяснение:
Объём пирамиды:
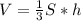, где S - площадь основания, h - высота пирамиды.
Значит 
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна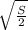 
Тогда, по теореме Пифагора:
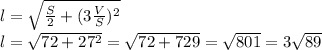
ответ: 1) <B=110°,<D=30°. 2) <B=<C=120°, <D=60°. 3) 9.
Объяснение:
1) Углы трапеции, прилегающие к одной из боковых сторон, в сумме дают 180°, как внутренние односторонние углы, поэтому :
<В=180°-<А=180°-70°=110°;
<D=180°-<С=180°- 150°=30°.
2) В равнобедренной трапеции углы при основании равны, значит <D=<A=60°.
AD║ВC по свойству оснований трапеции,
<A и <B - внутренние односторонние углы при AD║ВC и секущей АВ, значит <A+<B=180°.
<B=180°-<A=180°-60°=120°.
<C=<B=120° по свойству углов при основании равнобедренной трапеции.
3) <A=<D по условию, следовательно АВСD-равнобедренная трапеция по признаку, значит СD=АВ=9.
Дано: ABCD-прямоуг. трапеция, <ACD=90 градусов, СH-высота, BC=4 см, AD=16 см
Найти: <D-?, <C-?
Решение
45 градусов и 135 градусов будет
ну это получается так с вершины с проведем перпендикуляр вниз
се получится
найдем ед=ад-бс=16-4=4
по равенству треугольников треугольник абс=аес
значит се=4
т.к. се=4 и ед=4 треугольник сед = равнобедреный прямоугольный
а угол значит там 45 градусов
значит угол д =45
а вот угол с=180-45 градусов=135