по теореме синусов радиус описанной окружности равен
Площадь круга равна
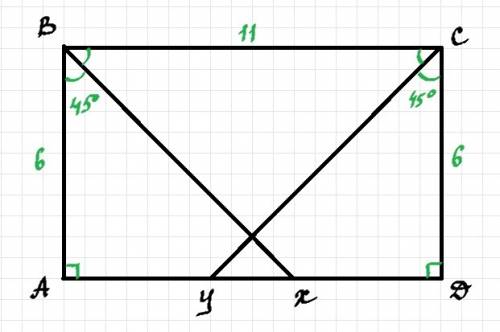
Рисунок к задаче в прикрепленном файле.
Рассмотрим ΔАВХ и ΔDCY.
Они прямоугольные, т.к. в прямоугольнике все углы прямые и ∠А=∠D=90°. АВ=CD, т.к. в прямоугольнике противоположные стороны равны. ∠АВХ=∠YCD, т.к. ВХ и CY биссектрисы и делят прямые углы В и С пополам (∠СВХ=∠ХВА=∠BCY=∠YCD=45°).
Следовательно ΔАВХ=ΔCDY (по катету и прилежащему острому углу). Эти треугольники равнобедренные, т.к. углы при основании у них равны.
АВ=АХ=YD=DC=6 (см).
АХ+YD=6+6=12 (см).
ВС=АD=11 см.
YX=АХ+YD-ВС=12-11=1 (см).
ответ: YX=1 см.
Висота = h = a x sin A (A - вместо угла альфа), т.к треугольник прямоугольный , а высота в равнобедренном треугольнике=медиане и биссектрисе
Половина основания = гипотенуза в квадрате - высота в квадрате =
= а в квадрате - (a x sin A) в квадрате =а в квадрате х (1 - sin A в квадрате)
Основание = 2 х а в квадрате (1 - sin A в квадрате) = 2 х а х (1 - sin A в квадрате) =
= 2 х а х (cos A в квадрате)
Площадь всего треугольника = 1/2 основания х высоту =
= 1/2 х 2 х а х (cos A в квадрате) х a x sin A = а в квадрате х (cos A в квадрате) х sin A
Радиус описаной окружности = ( а х b x c) /4S
Радиус описаной окружности = a x a x 2 х а х (cos A в квадрате) / а в квадрате х (cos A в квадрате) х sin A = (2 x a) /sin A