ответ: катеты 6√5 см и 12√5 см, гипотенуза 30 см. Синусы острых углов 1/√5 и 2/√5
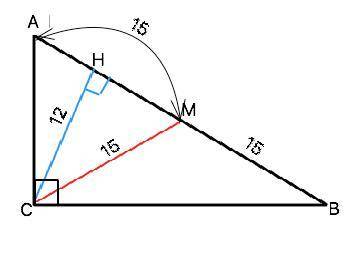
Объяснение: Сделаем согласно условию рисунок и обозначим вершины треугольника АВС ( угол С=90°).
СН=12 см - высота. СМ - медиана. По свойству медианы прямоугольного треугольника из прямого угла АМ=ВМ=СМ=15 см. =>
АВ=2•15=30 см
Из прямоугольного ∆ СНМ катет НМ равен 9 ( египетский). Тогда АН=АМ-МН=15-9=6 ⇒
из ∆ АНС по т. Пифагора АС= √(CH²+AH²)=√180=6√5
из ∆ ВНС по т. Пифагора ВС=√(CН²+BH²)=√720=12√5
Синус угла равен отношению противолежащего ему катета к гипотенузе.
sin ∠CAB=AC:AB=(6√5):30=1/√5 или ≈0,4472
sin ∠CBA=BC:AB=(12√5):30=2/√5 или ≈0,8944
Площадь пересечения плоскости с призмой равна площади треугольника ЕFP.
Площадь ΔЕFP = ½PH*EF
Найдем значение EF.
ΔЕР₁F подобен Δ M₁K₁P₁.
Все стороны ΔM₁K₁P₁ равны 4. При этом ЕР₁=½М₁Р₁=2 см.
⇒ все стороны ΔЕР₁F равны 2 : FP₁=EP₁=EF=2 см
EF=2
Найдем значение PH.
Из ΔЕАР выразим значение EP:
EP²=EA²+AP²
Так как боковое ребро правильной призмы равно 3, то ЕА=ММ₁=3 см
АР=МР/2 = 2 , где МР=4 см - сторона основания призмы.
EP²=9+4=13 см²
Из ΔЕРН выразим РН:
РН²=ЕР²-ЕН²=13-1=12 см²
PH=2√3 см
Посчитаем площадь ΔЕРF:
S ΔEPF = ½PH*EF= ½ * 2√3 * 2= 2√3 см²
ответ. Площадь пересечения призмы с плоскостью EFP равна 2√3 см²