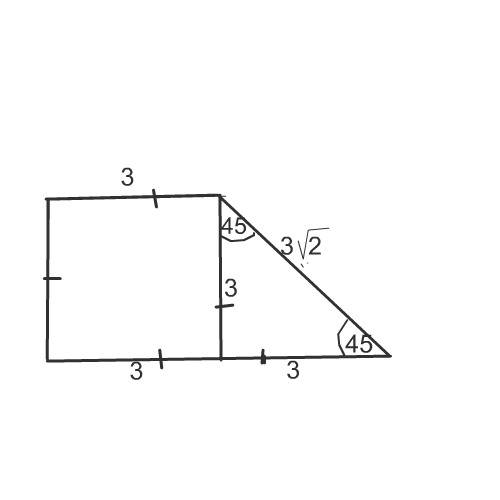
Сделаем рисунок к задаче.
Высота этой трапеции отсекает от нее прямоугольный равнобедренный треугольник с гипотенузой 3√2.
Такой треугольник - половина квадрата с диагональю=гипотенузе.
Формула диагонали квадрата ( формула гипотенузы равнобедренного прямоугольного тр-ка).
d=а√2, где а- сторона квадрата, а в равнобедренном прямоугольном треугольнике - катет. Знание этой формулы часто избавляет от лишних вычислений.
d=СК
СК =3√2=СН√2
СН√2=3√2
СН=3 см
СН=НК как равный катет.
АК=2НК
ВС=АК:2
Площадь трапеции равна Н*(АВ+ВС)
S=3*(3+6):2=13,5 см²
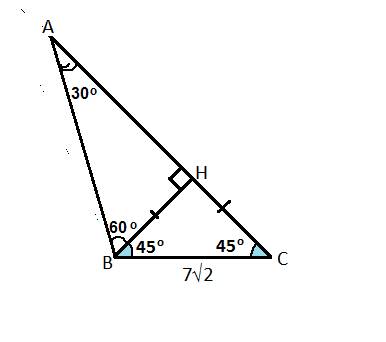
Чтобы прямая пересекала окружность, расстояние от центра окружности до прямой должно быть меньше радиуса окружности.
То есть ОН<r.
Если ОН=r, то прямая будет касаться окружности в точке Н.
Для наглядности на рисунке изображены четыре окружности разного радиуса и общим центром, из которого построен перпендикуляр к прямой. Отрезок ОН - расстояние от центра окружности до прямой.
1) Если радиус окружности r= 7 см, а расстояние ОН=9 см,
ОН>r. Прямая а не пересекает окружность с радиусом 7 см.
На рисунке такая окружность может быть желтого цвета. OR₁= 7 см
2) Если радиус окружности равен 9 см, то r=OH, и прямая касается окружности в точке Н. Розовая окружность.
3) Если радиус окружности равен 12 см, то ОН<r. И именно в этом варианте прямая пересекает окружность.
На рисунке это зеленая окружность.
4) При радиусе окружности 4,5 см, ОН>r ⇒ Прямая а не пересекает окружность. На рисунке это синяя окружность. ОR₂=4,5
ОТВЕТ: 3) Прямая пересекает окружность,если радиус окружности равен 12 см