Уравнение окружности. Урок 2 Найди, какие из данных уравнений являются уравнениями окружности.
Верных ответов: 3
8)x2 + y2 + 0,2x + 2,3y + 1,5 = 0
1)x2 + y2 – 5x – 3y + 12 = 0
4)x2 + y2 + 3x + 6y + 11 = 0
2)x2 + y2 + 7x – 2y – 10 = 0
3)x2 + y2 – 4x – 2y + 8 = 0
6)x2 + y2 – 3x + 8y + 19 = 0
7)x2 + y2 + 12x – 7y – 22 = 0
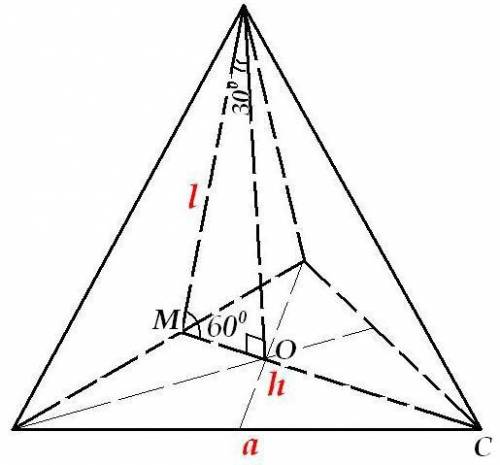
-сторона основания,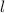 
- апофема, 
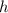- высота основания. Эти три величины потребуются для всего вычисления.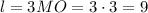
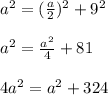
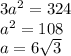
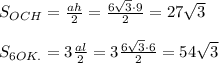
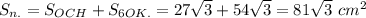
S=πRl+πR², ( l образующая)
Sполн.пов.=πR*(l+R)
1. сечение конуса - равнобедренный прямоугольный треугольник: гипотенуза - хорда х=6, катеты - образующие конуса l.
по теореме Пифагора:
x²=l²+l², 6²=l²+l², l²=18, l=3√2
2. осевое сечение конуса - равнобедренный треугольник основание - диаметр основания конуса d, боковые стороны - образующие конуса l.
по теореме косинусов: d²=l²+l²-2*l*l*cos120°
d²=18+18-2*√18*√18*(-1/2)
d²=54, d=3√6. R=1,5√6
S=π*1,5(√6*3√2+1,5)=1,5*π*(6√2+1,5)
S=1,5π*(6√2+1,5)