У параллелограмма всего 4 угла. В параллелограмме есть пара острых равных между собой углов, а также пара равных тупых углов (случай прямоугольника опустим, у него все углы равны, в этой задаче такого нет). Поэтому если мы найдем острый угол, а также тупой угол параллелограмма, то мы нашли все углы.
Теперь найдем их Ситуация следующая: есть две параллельные прямые, каждая из смежных с ними сторон является секущей. Получается, что имеются две пары односторонних друг для друга углов. Рассмотрим любую из них (для второй все то же самое)
Пусть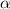 
- острый угол, 
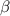- тупой. Тогда имеет место соотношение
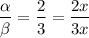
Известно, что сумма односторонних углов равна 180°, получаем вот такое уравнение:
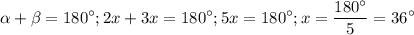
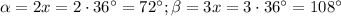
ответ: 72°, 72°, 108°, 108°
так как AD - биссектриса. Значит <DAC=(1/2)*<C. В треугольнике ADC <ADB - внешний и равен сумме двух внутренних углов, не смежных с ним, то есть <ADB=<DAC+<C или 1,5*<C=110°.
Тогда <C=110°:1,5=73и1/3°=<A, a <B=180°-146и2/3°=33и1/3° (так как сумма внутренних углов треугольника равна 180°).
ответ: <A=<C=73и1/3°, <C=33и1/3°.
P.S. Стоило в условии задачи дать <ADB=111° и мы получили бы ответ:
<A=<C=74°,a <B=32° !