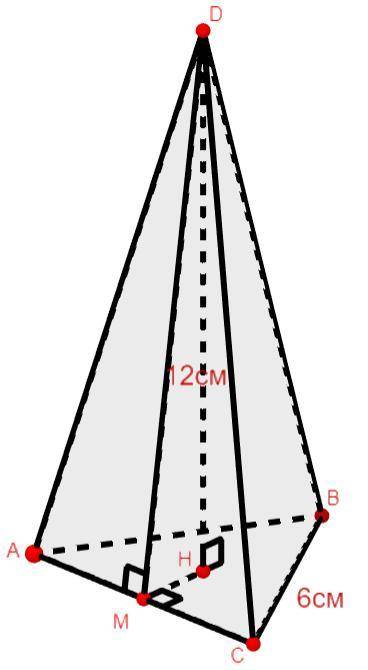
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
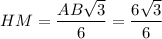=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
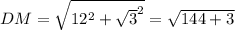=√147 см
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
Даны точки А (-2; 0; 5), В (2; -4; 5), С(0; -3; 2).
Найти:
a) Координаты векторов АВ и СВ.
АВ = (2-(-2); -4-0; 5-5) = (4; -4; 0).
СВ = (2-0; -4-(-3); 2-5) = (2; -1; -3).
б) Координаты вектора СВ = (2; -1; -3) и есть разложение:
СВ = 2i - j - 3k.
в) Длину вектора АВ = √(4² + (-4)² + 0²) = √32 = 4√2.
г) Координату середины отрезка АВ:
(1/2)АB = ((-2+2)/2; (0-4)/2; (5+5)/2) = (0; -2; 5)