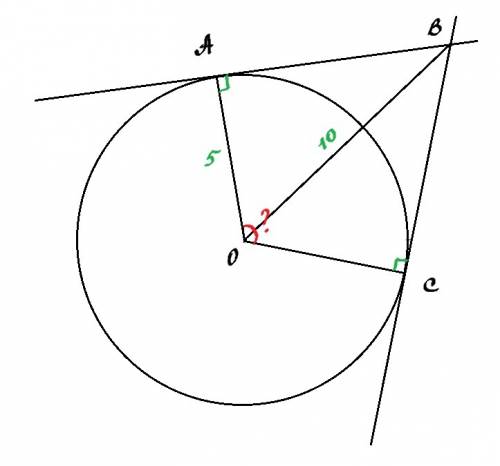
Рассмотрим ΔАВО. ОА - радиус окружности. ВА - касательная. Радиус окружности, проведенный в точку касания перпендикулярен касательной. Следовательно ΔАВО прямоугольный. ∠ОАВ = 90°.
ОА=5 - катет, ОВ = 10 - гипотенуза. Катет в два раза короче гипотенузы, следовательно он лежит напротив угла в 30°. Значит ∠АВО=30°, ∠АОВ=90°-30°=60°.
Рассмотрим ΔОВС. Он прямоугольный, т.к. радиус ОС проведен в точку касания, т.е. ОС⊥СВ. АО=ОС, т.к. являются радиусами окружности. ОВ - общая сторона треугольников АВО и ОВС. ΔАВО=ΔОВС по гипотенузе и катету.
Следовательно ∠АОВ=∠ВОС=60°.
∠АОС=∠АОВ+∠ВОС=60°+60°=120°.
ответ: ∠АОС=120°.
Пусть внешний угол равный 110° будет при вершине треугольника ( <A - вершина треугольника будет)
Тогда <A = 180 - 110 = 70°
Т.к. тр-к равнобедренный, то углы при основании равны (т.е. <B = <C). Т.к. сумма углов в тр-ке 180, найдём углы при основании:
180 - 70 = 110° - это произведение двух углов (<B и <C). Чтобы найти их по отдельности надо разделить получившееся число на 2: 110 / 2 = 55°
ответ: <A = 70°, <B=<C = 55°
Задача 2:
Вертикальные углы - пара углов, у которых общая вершина, а стороны одного угла составляют продолжение сторон другого (см. картинку)
Задача 3:
Через любую точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.