BK = 17см BC=11см
Объяснение:
BK+BC=KC
BK+BC=28 см
BK = BC+6см
BC+6+BC=28
2BC=28-6
2BC=22
BC=22/2
BC=11см
BK = 11+6
BK = 17см
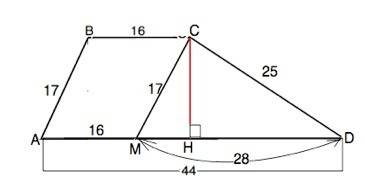
Назовем трапецию АВСD. АВ=17 см, ВС=16 см, СD=25 см, AD=44 см
Площадь трапеции равна произведению её высоты на полусумму оснований. Основания даны, высоту надо найти.
Один из решения:
Проведем СМ параллельно ВА. СМ=17 см (или ВК параллельно СD. Тогда ВК=25).
Получим треугольник, в котором известны три стороны: 17, 25 и 28 см.
По ф. Герона площадь этого треугольника равна 210 см².
Высота СН является и высотой трапеции.
S(∆ MCD)=CH•MD:2⇒
CH=2•S:MD=420:28=15 см
S(ABCD)=CH•(BC+AD):2=15•30=450 см²
Объяснение:
(28-6)/2=11см ВС
11+6=17см ВК