Расстояние от точки до прямой - длина перпендикулярного отрезка, проведенного между ними.
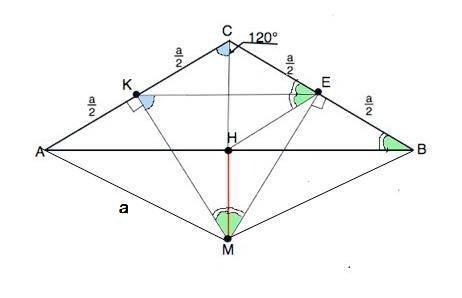
В равнобедренном ∆ АСВ углы при А и В равны (180°-120°):2=30°
К и Е - середины АС и ВС соответственно.
След. АК=КС=СЕ=ВЕ=а/2
КЕ║АВ по свойству средней линии.
∠СКЕ=∠СЕК=30° (соответственные углам А и В при пересечении параллельных КЕ и АВ секущими).
В четырехугольнике СКМЕ углы при К и Е равны 90° ( МК и МЕ - перпендикуляры)
. Сумма углов четырехугольника 360°. ⇒ ∠КМЕ=360°-2•90°-120°=60°.
∠ЕКМ=∠КЕМ=90°-30°=60°
∆ МЕК- равносторонний.
Срединные перпендикуляры треугольника пересекаются в одной точке. ⇒ СМ - срединный перпендикуляр, Н - середина АВ, и АН=ВН, ⇒
СН - медиана и биссектриса ∆ АСВ. ∠НСВ=60°
СН противолежит углу 30° ⇒ СН=СВ:2=а/2
СЕ=а/2, СН=а/2 ⇒∆ НСЕ- равносторонний, НЕ=а/2.
∠СМЕ=∠МЕН=30°
∆ МНЕ - равнобедренный. ⇒ МН⊥АВ, МН=ЕН=а/2.
* * *
Или короче:
Точка пересечения срединных перпендикуляров треугольника является центром описанной окружности.
МA=МC=МB - радиусы описанной окружности. .
Треугольник АМВ - равнобедренный и равен ∆ АСВ по трём сторонам. Острые углы при А и В этих треугольников равны и имеют градусную меру (180°-120°):2=30°
Поскольку угол МНА=90°, то из прямоугольного ∆ АНМ катет НМ=АМ•sin30°=a/2 (или, если больше нравится, то по свойству катета, противолежащего углу 30°, он равен половине гипотенузы АМ - равен а/2)
ответ:
объяснение:
1) 2*9=18- это две стороны по 9, 26-18=8/2=4-это другая сторона, s=9*4=36
2)s=a*a=169, a=13, p=13*4=52
3) s=a*b=96, 3*b=96, b=96/3=32, p=2(a+b)=2(3+32)=70
4)4a=164, a=164/4=41
6)a=x, b=6x, 2(x+6x)=70, 7x=35, x=5, 6x=6*5=30, a=5, b=30, s(пр)=5*30=150, s(кв)=150, (у равновеликих фигур площади равны),
s(кв)=a^2, a^2=150, a=v150=v(25*6)=5v6, p(кв)=4*5v6=20v6
7)s=a^2*v3/4=36*v3/4=9v3
У меня тоже такое давали