Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему. S = Pl/2. Апофема - высота боковой грани правильной пирамиды. Так как угол 45°, то и угол между апофемой и высотой пирамиды также 45°. Апофема равна высота делить на sin 45°, 3√2 :√2 /2 = 6. Найдем сторону квадрата (пирамида правильная), так как углы по 45°, то длина отрезка , соединяющего центр основания и апофему, равна высоте 3√2 , сторона квадрата равна двум отрезкам 6√2 , периметр 4·6√2 , полупериметр 12√2 , площадь боковой поверхности S = 12√2 ·3√2 = 72
Как известно, высота равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна её средней линии ( полусумме оснований).
Тогда h=(8+10):2=9 см
S=0,5•(8+10)•9=81 см²
Подробнее:
Диагонали равнобедренной трапеции равны. AC=BD
Так как они пересекаются под прямым углом, треугольники ВОС и АОД - равнобедренные прямоугольные, и тогда ВО=OC=ВС•sin45º=4√2 AO=OД=АД•sin45º=5√2, откуда
АС=ВД=4√2+5√2=9√2
Проведем высоту ВН.
НД=полусумме оснований (свойство равнобедренной трапеции)
. Т.к. угол ВДН=45°, треугольник ВНД- равнобедренный, ВН=НД=9√2*sin 45º=9
S АВСД=произведению полусуммы оснований на высоту.
S АВСД=0,5•(8+10)•9=81 см²
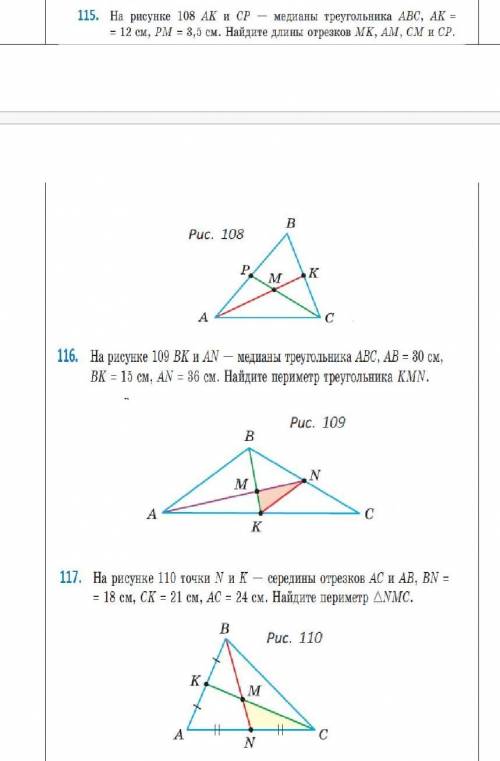
1. MK= 4 см, AM=8 см, CM=7 см и CP= 10,5 см.
2. 32 см.
Объяснение:
Теорема: Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1 , считая от вершины.
***
1. СМ=2РМ=2*3,5=7 см.
СР=3,5+7=10,5 см.
АК=12 см; АМ:МК=2:1
2х+х=12;
3х=12;
х=4 см - МК;
АМ=2*4=8 см.
***
2. AN=NC=24/2=12 см.
СМ=2/3 СК=2/3 *21=14 см.
MN=1/3 BN=1/3 *18=6 см.
РCMN=12+14+6=32 см.