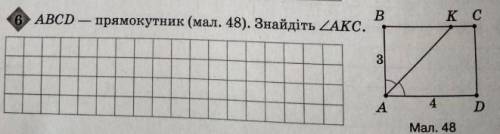
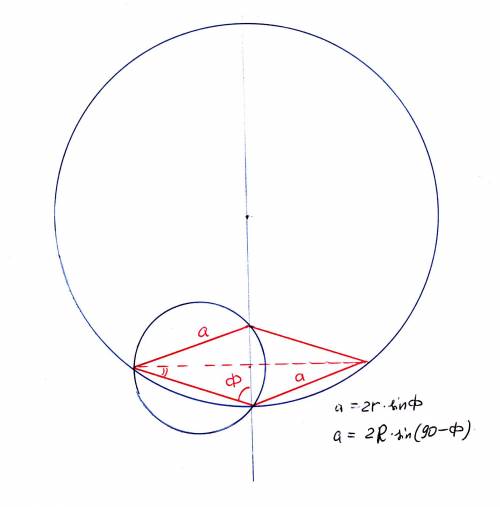
Меньшая окружность проходит через 3 вершины, одна из который - острый угол, а 2 - вершины тупых углов. Острый угол является вписанным в эту окружность. И, наоборот, большая окружность проходит через вершину острого угола, потом- тупого, и - опять острого. В большую окружность вписан тупой угол.
r = 5; R = 12; a = ?
Обозначим за Ф половину тупого угла ромба. В треугольнике, вписанном в малую окружность, это будет острый угол, противолежащий стороне а;
Тогда по теореме синусов
a = 2*r*sin(Ф); sin(Ф) = a/(2*r);
Для тупоугольного равнобедренного треугольника, вписанного в большую окружность, угол при основании (противолежащий стороне а) равен (180 - 2*Ф)/2 = 90 - Ф;
Поэтому по той же теореме синусов
a = 2*R*sin(90 - Ф) = 2*R*cos(Ф); cos(Ф) = a/(2*R);
Осталось возвести это в квадрат и сложить
1 = a^2/(2*r)^2 + a^2/(2*R)^2; (2/a)^2 = 1/r^2 + 1/R^2;
Нет смысла упрощать это выражение в общем виде, подставим числа.
2/a = корень(1/25 + 1/144) = 13/60; (опять пифагорова тройка 5,12,13)
a = 120/13;
Оба случая очень простые, не понятно, почему эта задача вызывает проблемы.
Есть окружность радиуса r и две касательных к ней, проведенных из точки А вне окружности. Обозначим В и С точки касания. По свойствам касательных АВ = АС, и АВ перпендикулярно ОВ, АС перпендикулярно ОС, где О - центр окружности. Проведем прямую АО. По свойству биссектрисы каждая её точка равноудалена от сторон угла, поэтому АО - биссеткриса угла САВ (точка О обязательно лежит на биссетрисе, а через А и О можно провести только одну прямую).
Итак, угол ВАО = угол САО. Прямоугольные треугольники ВАО и САО, очевидно, равны - у них общая гипотенуза и равные острые углы, катеты, и вообще все...:))
Теперь рассмотрим отдельно оба случая.
1. r = 5, угол ВАС = 60 градусам. В этом случае треугольник АОВ имеет угол в 30 градусов (угол ВОА) против стороны ВО. Поэтому АО = 2*ВО = 10.
(Кстати, если не понятно, почему, можно проделать мысленно интересную штуку - попробуйте повернуть весь треугольник ОСА вокруг точки А по часовой стрелке, пока АС не совпадет с АВ. У вас получится равносторонний треугольник, поскольку ОС попадет точно на продолжение ОВ - это легко увидеть из равенства углов. Поэтому ОВ = ОС = АВ/2 :))
2. ОА = 14, угол ВАС = 90 градусов. В этом случае фигура АВСО - квадрат, и ОА - его диагональ, а ВО = СО = (конечно же, в этом случае) = АВ = АС - это радиус окружности. По теореме Пифагора (ну, если так просили, почему бы нет:))
АВ^2 + BO^2 = AO^2; 2*r^2 = 14^2; r = 7*корень(2)/2