В основании пирамиды лежит правильный треугольник со стороной 5 см. Основание высоты Пирамиды равноудалено от сторон этого треугольника. Высота одной из боковых граней равна 10 см. Вычислить боковую поверхность пирамиды.
Объяснение:
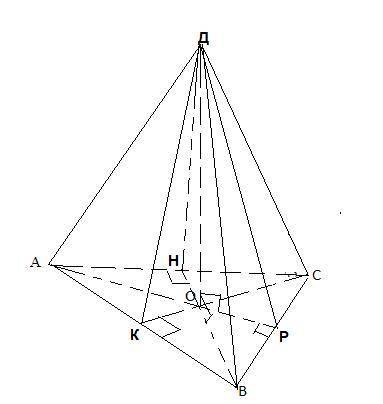
АВСД-пирамида, ДО-высота пирамиды .Пусть ДК⊥АВ, ДР⊥ВС, ДН⊥АС.
Т.к. О-основание высоты пирамиды равноудалено от сторон треугольника, то О-центр вписанной окружности и расстояние от О до стороны треугольника это r-вписанной окружности.
Тогда высоты всех боковых граней(т.е апофемы ) равны, т.к прямоугольные ΔДОК=ΔДОР=ΔДОН по двум катетам ДО-общая, ОК=ОР=ОН=r.
S(бок.)=1/2*Р(осн.)*а , где а-апофема .
Р=3*5=15 (см).
S(бок.)=1/2*15*10=75 (см²)
E=F=90 (вписанные углы, опирающиеся на диаметр)
CEDF - прямоугольник, DF=EC=50, DE=FC=20
CD^2 =50^2 +20^2 (т Пифагора)
CDF =90-BDF =B
CDF~DBF (по двум углам)
CD/DB =CF/DF => DB =CD *50/20
Аналогично AD =CD *20/50
S(ABC) =1/2 AB*CD =1/2 (AD+DB) CD =1/2 *CD^2 (2/5 +5/2) =4205
Или (то же самое)
B =ADE =CDF
tg(CDF) =CF/DF
AD=CD*tgB, DB=CD*ctgB
S(ABC) =1/2 (AD+DB) CD =1/2 CD^2 (tgB +ctgB)