Если вас еще интересует решение этой задачи, то здесь не так уж и сложно.
Нужно воспользоваться формулами для нахождения диагоналей параллелограмма через его стороны.
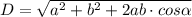
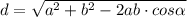
D - большая диагональ, d - малая диагональ.
Подставляем длины сторон и диагоналей и находим угол 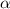
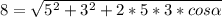
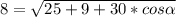
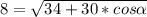
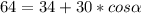
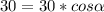
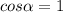

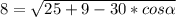

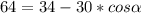
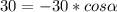
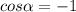
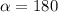
Как видим, углов между сторонами 5 и 3, при которых одна из диагоналей могла бы равняться 8, и при которых сещуствовал бы параллелограмм, нет.
Вот и вывод: диагональ параллелограмма не может равняться 8 при сторонах 5 и 3.
Теорема d3. В равнобедренном треугольнике высоты, опущенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его высоты. Тогда углы ABL и KAB равны, так как углы ALB и AKB прямые, а углы LAB и ABK равны как углы при основании равнобедренного треугольника. Следовательно, треугольники ALB и AKB равны по второму признаку равенства треугольников: у них общая сторона AB, углы KAB и LBA равны по вышесказанному, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Если треугольники равны, их стороны AK и BL тоже равны. Что и требовалось доказать
Объяснение:
5
5
6
Объяснение:
средняя линия - половина основания (получили 6)
треуг - равнобедренный (16-6 и пополам)