Так как биссектриса острого угла A прямоугольного треугольника ABC не может быть перпендикулярна BC, то биссектриса угла A и серединный перпендикуляр к BC имеют ровно одну общую точку.
Пусть N — середина BC. Рассмотрим окружность, описанную около треугольника ABC. Пусть серединный перпендикуляр к BC пересекает меньшую дугу BC в точке L (см. рисунок), тогда точка L является серединой этой дуги, ⌣BL = ⌣LC. Но тогда \angle BAL= \angle CAL как вписанные углы, опирающиеся на равные дуги, а отсюда AL — биссектриса \angle BAC. Но это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой \angle BAC. Заметим, что \angle BCL= \angle CBL как вписанные углы, опирающиеся на равные дуги.
Пусть \angle BCL= x. Четырехугольник ACLB — вписанный, поэтому \angle ACL плюс \angle ABL = 180 в степени circ, то есть 40 в степени circ плюс x плюс 90 в степени circ плюс x = 180 в степени circ , откуда x = 25 в степени circ. Так как точки K и L совпадают, \angle BCK = \angle BCL = 25 в степени circ.
ответ: 25°.
Раздел кодификатора ФИПИ: Углы в окружностях
Угол, косинус которого имеет отрицательный знак, - тупой. Он – смежный острому углу с таким же косинусом со знаком "+".
cos(180°-α)= -cosα
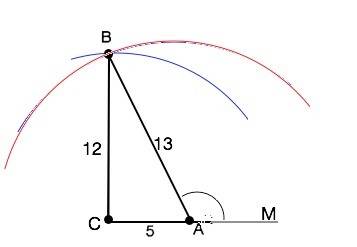
Построим острый угол с положительным косинусом 5/13. Смежным ему будет тупой угол с данным в условии косинусом -5/13.
Косинус - отношение в прямоугольном треугольнике катета , прилежащего к данному углу, к гипотенузе.
Для этого построения нам надо найти второй катет прямоугольного треугольника, в котором один катет равен 5, гипотенуза - 13.
Пусть нам надо построить треугольник АВС с прямым углом С.
Известны гипотенуза АВ=13, катет АС=5
По т. Пифагора ВС²=АВ²-АС²
ВС=√(169-25)=12
Построение. На луче СМ отложим отрезок АС=5
Из точки А как из центра чертим полуокружность радиусом 13 см.
Из точки С как из центра чертим полуокружность радиусом 12 см.
Точку их пересечения обозначим В.
Соединим А и В. Косинус угла ВАС=АС:АВ=5/13.
Косинус смежного ∠ВАМ= -5/13. Это искомый угол.
Из точки С по общепринятому методу возводим перпендикуляр. На нем откладываем катет СВ=12 см.
Соединяем В и А. В построенном треугольнике косинус угла А равен 5/13. Смежный ему тупой угол ВАМ - искомый, его косинус - 5/13.
∠BAD= 91
∠B= 109
∠BCD= 91
∠D=109
Объяснение:
∠BAD=∠BAC+∠CAD, ∠BCA=∠CAD т.к накрест лежащие поэтому ∠BAD=∠BAC+∠BCA=34+57=91
∠B=180-∠A, ∠A=∠BAC+∠CAD=34+57=91, ∠B=180-91=109
∠BCD=∠A=91 так как в параллелограмме противолежащие углы равны.
∠D=∠B=109