2. Сумма углов восьмиугольника вычисляется по формуле: 
. Разделив это число на 8, найдем чему равен один угол. 
. По определению, внешний угол это угол, смежный с любым внутренним. А так как сумма смежных углов равна 180 градусам, получаем: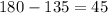 
, что и сходится с утверждением.
3. Разобьем параллелограмм на четыре треугольника путем проведения в нем диагоналей. Для произвольного треугольника на плоскости всегда выполняется неравенство треугольника: сумма длин двух сторон больше или равна длине третьей. Дальше все понятно, во вложении.
5. У правильного многоугольника с нечентым числом сторон осями симметрии являются прямые, выходящие из вершин углов, которые перпендикулярны противолежащей углам сторонам. Для правильного многоугольника точка пересечения этих прямых будет являться центром описанной окружности. А по свойству тех же правильных многоугольников, это точка будет еще и центром вписанной окружности. Следовательно, центр вписанной окружности является центром симметрии пятиугольника.
Хорда АВ, диаметр АД, О -центр, проводим радиус ОВ, треугольник АВО раносторонний, АВ=ОА=ОВ=радиусу, все углы в треугольнике =60
№2
дуга ВС = дуга АВ-дуга АС=125-52 =73, угол ВАС=1/2 дуги ВС=73/2=36 град 30 мин
хорда АВ ближе к центру
№3
проводим радиус ОВ перпендикулярный АВ в точку В, ОВ=15, АО=17, треугольник АОВ прямоугольный, АВ= корень(АО в квадрате - ОВ в квадрате) = корень(289-225)=8
№4
дугаАВ+дугаВС+дугаАС =360, 7+5+6=360, 18 частей =360, 1 часть =360/18=20
дугаАВ=7 х 20 =140, угол АОВ центральный = дугеАВ =140
дуга ВС =5 х 20 =100, угол ВАС вписанный=1/2 дуги ВС = 100/2=50
дуга АС = 6 х 20 =120, угол АВС вписанный = 1/2 дуги АС= 120/2=60
№5
АВ - диаметр = 10+10=20, СД хорда , СМ=4, МД=9
АМ х МВ = СМ х МД, АМ = а, МВ = 20-а
а х (20-а) = 4 х 9, 20а - а в квадрате=36, а в квадрате - 20а + 36 =0
а= (20+-корень(400 - (4 х 36))/2
а =(20+- 16)/2
а1 = 18
а2=2
а = АМ =2
МВ=20-2=18
№6
треугольник АВС, АВ=ВС=15, АС = 18
площадь = корень (p x (p-a) x (p-b) x (p-c)). где р - полупериметр, остальное стороны
полупериметр = (15+15+18)/2=24
площадь = корень (24 х (24-15) х (24-15) х (24-18) = корень 11664 = 108
радиус вписанной окружности = площадь / полупериметр = 108/24=4,5
радиус описанной окружности= произведение сторон / 4 х площадь =
=15 х 15 х 18 / 4 х 108 = 4050/432=9,375