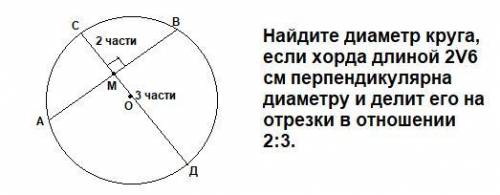
Найдите диаметр круга, если хорда длиной 2V6 см перпендикулярна диаметру и делит его на отрезки в отношении 2:3.
Объяснение:
ΔОМА=ΔОМВ как прямоугольные по двум катетам ОМ-общий, ОА=ОВ как катеты ⇒МА=МВ=2√6:2=√6 (см)
По т. об отрезках пересекающихся хорд АМ*МВ=СМ*МД
Т.к. СМ/МД=2/3 , то МД=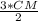 
. Получим √6*√6= СМ* .
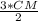СМ²=4, СМ=2 см .
Тогда МД=3 см , поэтому диаметр равен d= СМ+МД=2+3=5 (см).
d=5 см
=====================
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
построим прямую OA от точки O до прямой MH так что угол OAM = 90 градусов,
это и есть расстояние от точки O до прямой MН
Треугольники MOA и MOK равны это следует из следующего :
1 в треуг ОАМ угол OAM = 90 гр
в треуг OMK угол OKM = 90 гр
2 угол АMO = углу KMO (биссектриса угла)
3 сторона треугольника MO общая для обоих треугольников
4 также угол MOA и угол MOK в обоих треуг. равны, поскольку
сумма углов в треуг. = 180 гр. ( вычитая 180 - 90 гр - известный угол)
Этих условий достаточно чтобы сделать вывод, что треугольники равны.
Следовательно OK = OA = 9
ответ 9
Объяснение:
угол 1 равен углу 2 значит 63°С [Так как они вертикальны]
угол3 равен углу 4 значит 180-63 = 117°С
ответ: градусную меру всех углов составляет117°С и 63°С