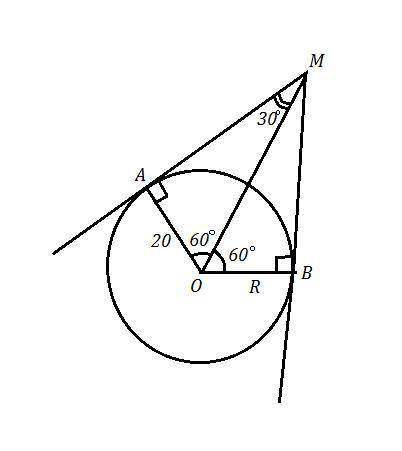
Дана окружность с центром в точке О . Её радиус R=20 см .
АМ и ВМ - касательные к окружности. По свойству, они перпендикулярны радиусу R , то есть АМ⊥ОА и ВМ⊥ОВ .
Дуга ВА=120° ⇒ ∠АОВ=120° ,как центральный угол, опирающийся на дугу ВА .
ОМ - биссектриса ∠АОВ ( по свойству ) ⇒ ∠АОМ=∠ВОМ=120°:2=60°
ΔАОМ - прямоугольный и ∠АМО=180°-90°-60°=30° .
В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы ⇒ ОА=1/2*ОМ ⇒
ОМ=2*ОА=2*20=40 см - это расстояние от точки М до центра окружности .
При пересечении двух прямых образовались 4 угла,и эти четыре угла равны 360 градусов,получилось две пары вертикальных углов
<АОD=<COB,как вертикальные
<АОС=<DOB,как вертикальные
<АОD=X
<COB=X
<AOC=2X
<DOB=2X
X+X+2X+2X=360 градусов
6Х=360
Х=360:6
Х=60
<АОD=<COB=60 градусов
<АОС=<DOB=60•2=120 градусов
Объяснение:
Вопрос стоит так-сумма двух углов равна градусной мере третьего угла
Два вертикальных угла по 60 градусов,а один угол из другой пары вертикальных углов равен 120 градусов
60+60=120 градусов,что и следовало доказать