Фактически задача сводится к нахождению координат вектора CD.
Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.
Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.
Формула косинуса угла между векторами - 
AB={-1+5;4-1}={4;3}
CD={x2-3;y2-2}
Составим уравнение прямой АВ: 
(*)
Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:
4(x2-3)+3(y2-2)=0
Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).
Решаем полученную систему уравнений.
Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.
Оно выглядит так: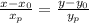 
, где 
- координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)
ПАРАЛЛЕЛЬНОЕ ПРОЕКТИРОВАНИЕ
В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно в геометрии для этого используется параллельное проектирование.
Пусть p - некоторая плоскость, l - пересекающая ее прямая (рис. 1). Через произвольную точку A, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью p называется параллельной проекцией точки A на плоскость p в направлении прямой l. Обозначим ее A'. Если точка A принадлежит прямой l, то параллельной проекцией A на плоскость p считается точка пересечения прямой l с плоскостью p.
Таким образом, каждой точке A пространства сопоставляется ее проекция A' на плоскость p. Это соответствие называется параллельным проектированием на плоскость p в направлении прямой l.
Пусть Ф - некоторая фигура в пространстве. Проекции ее точек на плоскость p образуют фигуру Ф', которая называется параллельной проекцией фигуры Ф на плоскость p в направлении прямой l. Говорят также, что фигура Ф' получена из фигуры Ф параллельным проектированием.
Примеры параллельных проекций дают, например, тени предметов под воздействием пучка параллельных солнечных лучей.
Рассмотрим свойства параллельного проектирования.
Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
Доказательство. Ясно, что если прямая k параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой на плоскость p будет точка пересечения прямой l и плоскости p. Пусть k не параллельна и не совпадает с прямой l (рис. 2). Возьмем какую-нибудь точку A на прямой k и проведем через нее прямую a, параллельную l. Ее пересечение с плоскостью проектирования p даст точку A', являющуюся проекцией точки A. Через прямые a и k проведем плоскость a . Ее пересечением с плоскостью p будет искомая прямая k', являющаяся проекцией прямой k.