Даны : отрезок, равный периметру АР треугольника АВС и два угла этого треугольника:
угол ВАС, угол ВСА. Построить по этим данным треугольник АВС.
Вариант решения.
построение угла, равного данному, стандартный, описан не раз и не является целью решения данной задачи.
От т.А откладываем стандартным угол, равный углу ВАС.
От произвольной точки К на АР откладываем угол, равный углу ВСА. Точку пересечения их сторон обозначим М. На АН от т.А откладываем циркулем АТ=АК , ТЕ=АМ и ЕН=МК; отрезок АН. равен сумме сторон треугольника АМК, т.е. периметру ∆АМК.
Соединим Н и Р. Проведем параллельно НР прямую из т.Т до пересечения с АР, обозначим точку пересечения С. Треугольник АНР и АТС подобны - общий угол и параллельные стороны НР и ТС. Коэффициент подобия равен отношению периметров ОАР1Р и О.
По т.Фалеса параллельные прямые на сторонах угла отсекают пропорциональные отрезки.
АТ:АС=АН:АР. ⇒ АС - сторона искомого треугольника АВС.
От С проведем СВ║КМ. Точку пересечения обозначим В.
∠ВСА=∠МКА как соответственные, угол А - равен данному по построению.
Построенный треугольник АВС равен искомому по стороне и двум углам.
* * *
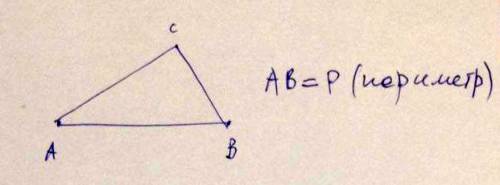
Построим отрезок AB, равный периметру P. Из точек A и B под известными углами проведём лучи до пересечения в точке C.
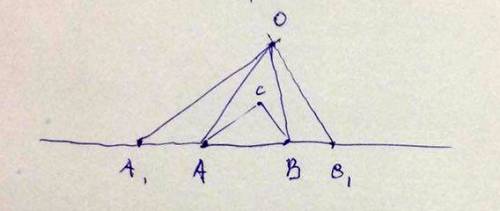
На прямой AB от точки A отложим отрезок AA1, равный AC, от точки B отложим отрезок BB1, равный BC.
Теперь, как и в первый раз построим треугольник по известным углам, но уже на основании A1B1, лучи пересекутся в точке O.
Дальше соединим вершину O с точками A и B. Затем на стороне OA1 от точки O отложим отрезок, равный AC, на стороне OB1 от точки O отложим отрезок, равный BC.
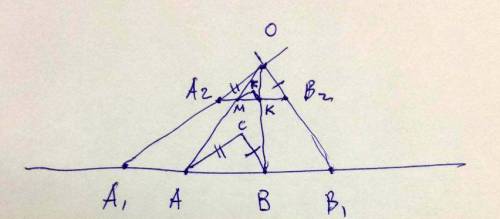
Получившийся треугольник A2OB2 равен треугольнику ACB по двум сторонам и углу между ними. Его основание разбито отрезками OA и OB на отрезки A2M, MK и KB2, пропорциональные сторонам треугольника ACB.
На основании MK по трём сторонам построим треугольник MFK (в качестве двух недостающих сторон возьмём A2M и KB2).
Стороны получившегося треугольника пропорциональны сторонам треугольника ACB, значит, они подобны, значит их соответствующие углы равны, а его периметр равен P. Значит, это искомый треугольник.