
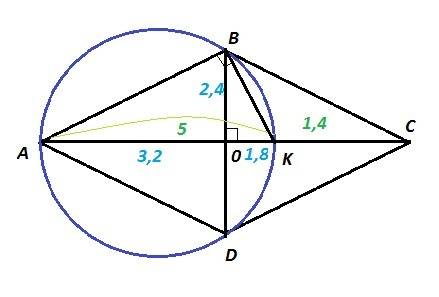
Ромб ABCD, окружность проходит через точки A, B, C
AK = 5 см; КС = 1, 4 см ⇒ АС = АК + КС = 5 + 1,4 = 6,4 см
У ромба диагонали перпендикулярны и точкой пересечения делятся пополам : AC⊥BD; AO=OC = AC/2 = 6,4 /2 = 3,2 см; BO=OD.
AK⊥BD и делит хорду BD пополам ⇒ AK - диаметр окружности.
ΔABK - прямоугольный, так как сторона AK является диаметром описанной окружности.
Высота треугольника, проведенная из прямого угла на гипотенузу, есть среднее геометрическое проекций катетов на гипотенузу :
BO² = AO·OK = AO·(AK-AO) = 3,2·(5-3,2) = 3,2·1,8 = 5,76 = 2,4²
BO = 2,4 см
ΔAOB образован диагоналями, прямоугольный. Теорема Пифагора
AB² = AO² + BO² = 3,2²+2,4² = 10,24+5,76= 16 = 4²
AB = 4 см
ответ: сторона ромба равна 4 см
Боковая сторона равнобедренного треугольника равна 10 см, а его основание 12 см. Найдите его площадь.
Биссектриса угла А параллелограмма ABCD делит сторону ВС на отрезки ВК и КС, равные соответственно 8 см и 4 см. Найдите периметр параллелограмма.
В трапеции ABCD углы А и В прямые. Диагональ АС — биссектриса угла А и равна 6 см. Найдите площадь трапеции, если угол CDA равен 60°.
В окружности проведены две хорды АВ и CD, пересекающиеся в точке К, КС = 6 см, АК = 8 см, ВК + DK = 16 см. Найдите длины ВК и DK.
Квадрат со стороной 8 см описан около окружности. Найдите площадь прямоугольного треугольника с острым углом 30°, вписанного в данную окружность.