Дано:
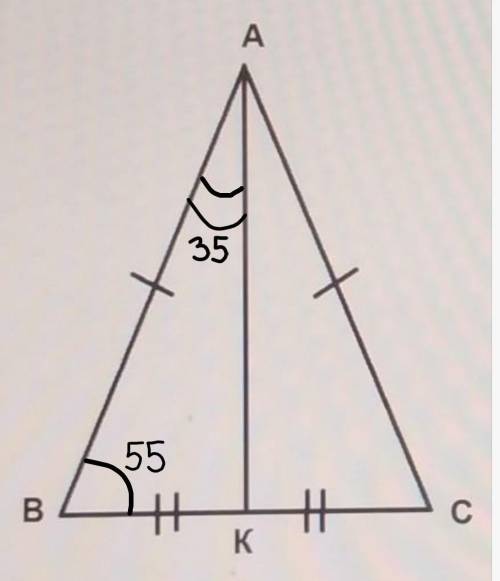
AB = AC
угол BAK = 35°
BC = 10 см
ВК = KC
угол ABC = 55°
Найти:
ВК, угол KAC, угол BAC, угол AKB, угол ACB
ВС=ВК+КС, так как ВК=КС по условию, то ВК=ВС÷2. ВС=10 см по условию, тогда ВК=10÷2=5 см.
Так как АВ=АС по условию, то ∆АВС – равнобедренный с основанием ВС.
Углы при основании равнобедренного треугольника равны, то есть угол АСВ=угол АВС=55°
Так как ВК=КС, то АК – медиана проведенная к ВС.
Медиана, проведённая к основанию равнобедренного треугольника, так же является биссектрисой и высотой. Следовательно АК – биссектриса, тогда угол КАС=угол ВАК=35°, угол ВАС=угол ВАК*2=35°*2=70°. И угол АКВ=90°.
ответ: 5 см, 35°, 70°, 90°, 55°.
В прямоугольном равнобедренном треугольнике угол между катетом и гипотенузой равен 45 градусов. Тангенс равен 1.
Используем формулу угла между прямыми по угловым коэффициентам.
Угловой коэффициент заданной прямой равен k₁ = (-2/3).
tg φ = (k₂ - k₁/(1 + k₁*k₂). Приравняем тангенс 1.
1 +(-2/3)*k₂ = k₂ - (-2/3),
(5/2)k₂ = 1/3,
k₂ = 1/5.
Уравнение катета СА имеет вид у = (1/5)х + в.
Для определения параметра в подставим координаты точки С(2; -1).
-1 = (1/5)*2 + в,
в = -1 - (2/5) = -7/5.
Получаем уравнение катета СА: у = (1/5)х - (7/5).
Угловой коэффициент катета СВ k₃ = -1/k₂ = -1/(1/5) = -5.
Уравнение катета СВ имеет вид у = (-5)х + в.
Для определения параметра в подставим координаты точки С(2; -1).
-1 = (-5)*2 + в,
в = -1 + 10 = 9
Уравнение катета :СВ у = (-5)х + 9.