P=36см
Объяснение:
т.к у паралел. парлельные стороны попарно равны то его P=(6+12)×2=36
Построение сечения: Назовем искомую плоскость MNK 
. Плоскости ABC и A1B1C1 параллельны и пересечены плоскостью , следовательно, линии пересечения параллельны. Значит, пересекает А1В1С1 по прямой КF, параллельной MN. Значит, F - середина А1В1. Осталось соединить KF, FM, MN, NK. Искомое сечение - FKNM.
Доказательство: В треугольнике ABD MN-средняя линия, MN || BD. Т.к MN лежит в плоскости сечения MNK, а BD параллельна прямой MN, лежащей в плоскости сечения, ВD параллельна плоскости MNK, что и требовалось доказать.
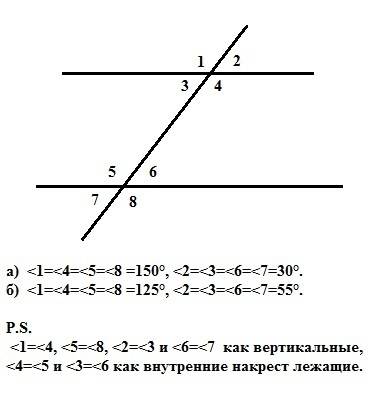
Углы, образованные при пересечении двух параллельных прямых секущей, или равны, или в сумме составляют 180°. Следовательно, нам дано значение одного из смежных углов.
а) второй угол равен 180° - 150° =30°.
б) один из углов равен Х градусов, второй - Х+70 градусов. Их сумма равна 2Х+70=180° => X=55°. Тогда меньший угол = 55°, второй = 125°.
Или (см. рисунок): а) <1=<4=<5=<8 =150°, <2=<3=<6=<7=30°.
б) <1=<4=<5=<8 =125°, <2=<3=<6=<7=55°.
P.S.
<1=<4, <5=<8, <2=<3 и <6=<7 как вертикальные,
<4=<5 и <3=<6 как внутренние накрест лежащие.
Тридцать шесть
Объяснение:
12+12+6 +6=36