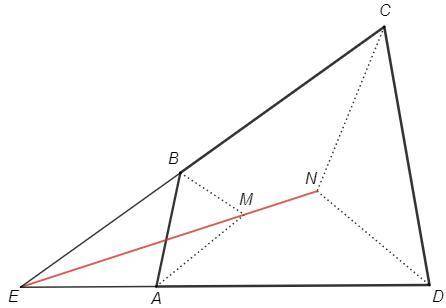
1) AD не параллельна BC, они пересекаются в точке E.
M - точка пересечения биссектрис внешних углов △AEB =>
M лежит на биссектрисе ∠E.
N - точка пересечения биссектрис △CDE =>
N лежит на биссектрисе ∠E.
Если MN перпендикулярна AB, то в △AEB совпадают биссектриса и высота.
Тогда △AEB - равнобедренный, углы при основании равны.
Углы A и B четырехугольника равны как смежные с равными.
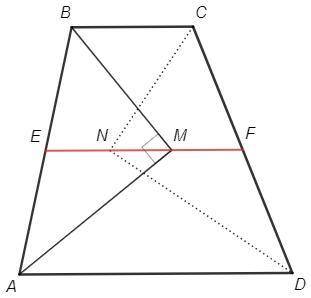
2) AD параллельна BC, трапеция.
Биссектрисы внутренних углов при параллельных пересекаются под прямым углом.
Пусть E - середина AB.
ME - медиана из прямого угла, ME=AB/2
△BEM - равнобедренный, ∠EMB=∠EBM=∠CBM
ME||BC (по накрест лежащим) => M лежит на средней линии трапеции.
Аналогично N.
Если средняя линия перпендикулярна боковой стороне, то трапеция прямоугольная, ∠A=∠B=90.
Дано: шар с центром в точке
R=13- радиус шара
плоскость а -сечение шара
р(а, О)=5 (расстояние от центра шара О до плоскости а
Найти: r-радиус круга в сечении
Решение
Сечением будет круг. Найдем его радиус. От центра шара до центра сечения 5 - это катет треугольника, который получится, если соединим центр шара, центр сечения и точку пересечения шара с его сечением. 13 - гипотенуза, по теорПифагора:r=√13²-5²=√144=12. S=πr²=π144=144πкв.ед