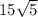 (кв. единица)
(кв. единица)
Объяснение:
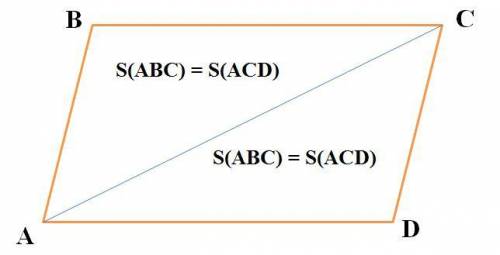
По условию задано координаты трёх его вершин параллелограмма АВСD: А(27;18;20) , В(24;18;16) и С(18;21;18). Так как верно свойство (см. рисунок) "Диагональ параллелограмма делит его на два равных треугольника", то площадь параллелограмма S(ABCD) равна удвоенной площади одного из треугольников, то есть
S(ABCD)=2·S(ABC).
В нашем случае диагональ AC делит параллелограмм на два равных треугольника. Поэтому достаточно найти площадь S(ABC) треугольника ABC по формуле Герона:
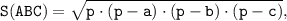
где p - полупериметр: 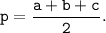
Стороны треугольника ABC находим по формуле расстояния между двумя точками с координатами M(x₁; y₁; z₁) и N(x₂; y₂; z₂):
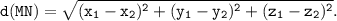
Так как А(27;18;20), В(24;18;16) и С(18;21;18), то
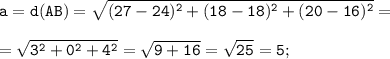
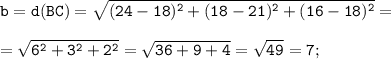
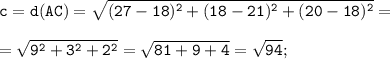
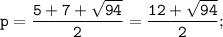
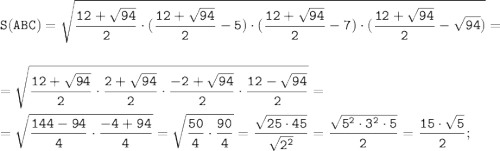
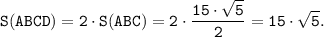
из суммы углов тр-ка
уг А+ уг В+ уг С=180
уг В=180-75-35=70
ВД - биссектриса, делит угол поплам или 70/2=35 - этому значению равен один из углов тр-ка ВДС, а вместе с этим уг С=35 гр. отсюда углы при основании тр-ка равны из этого следует треугольник ВДС раванобедренный