Объем конуса с радиусом 12 см увеличился на 125%, при этом высота осталась неизменной. найдите новый радиус конуса. варианты: 30, 24, 15, 18см. заранее
Т у это ранобедреный треугольник то бисиктриса медиана и высота проведёного из большего угла это одно и тоже, а т к это прямоугольный треугольник , то бисиктриса его большего угла =45 градусов , а т к мы провель медиану,высоту,бесиктрису из этого угла , то меньшие углы этого прямоугольного треугольника будут равны по 45 градусов)
исходя из вышеданого можно найти катиты прямоуг треугольника т к он равнобедреный ,то формула его катитов будет такова катит = корень квадратный()=корень из 9=3 делил на половину т к катиты одинаковые а всё остальное по теоремепифагора гипотинуза в квадрате =1катит в квадрате+2катит в квадрате
Так как по условию задачи треугольник прямоугольный, то один из углов = 90° Сумма углов в треугольнике равна 180° Так как по условию задачи гипотенуза равна 3√2, а треугольник равнобедренный, то катеты равны и углы при катетах равны: (180°- 90°):2=45° Найдём один из катетов: 3√2·сos45°=3√2·√2/2=6:2=3 см. Так как треугольник равнобедренный и катеты равны, то оба катета = 3см. ответ: острые углы=45°, катеты=3см
Р.s.: √2/2 пишите дробью, у меня здесь нет этой функции - √2 в числителе (сверху), а 2 в знаменателе (внизу под дробью). Можете все обозначить буквами. треугольник АВС, угол А=90°, найти острые углы В и С. Тогда катетами будут АВ и АС
Объем конуса равен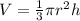
Первый объем меньше второго (изменившийся) ((100+125)/100)=2,25
r1=12
r2=18