радиус окружности - R
S∆ =R^2*3√3/4
S□ = (2R/√2)^2=2R^2
S□ - S∆ = 18.5 = 2R^2 - (R^2*3√3/4) = R^2 (2 -3√3/4 )
R^2 (2 -3√3/4 ) = 18.5
R^2 = 18.5 / (2 -3√3/4 )
сторона правильного шестиугольника равна радиусу описанной окружности
шестиугольник состоит из 6 равносторонних треугольника
площадь шестиугольника
S(6) = 6*1/2*R^2*sin60=3*18.5 / (2 -3√3/4 )*√3/2=6√3*18.5 / (8 -3√3)=
= 111√3 /(8 -3√3) = 111√3 *(8+3√3) / (8-3√3) (8+3√3) =
= 27+24√3 = 24√3+27
= 3(9+8√3)= 3(8√3+9)
** ответы на выбор
описаная окружность, тогда образуется три равные дуги с центр углом 120 град,
тогда площадь треуг = 3*1/2*R*R*sin 120=
=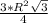
Квадрат состоит из 4 равных треугольников, причем радиусы - половины диагоналей образуют угол 90 град, тогда
Sквадрата =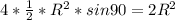
Sквадр - Sтреуг=18,5, подставим, получим :
В описанной окружности правильного шестиугольника получается 6 равносторонних треугольника со стороной = R, тогда
Sшестиуг =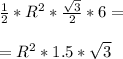
Подставим значение R^2, получим :
Sшестиуг=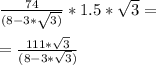
ответ: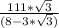
Домножив числитель и знаменатель на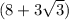
получим: