Примем сторону куба равной а.
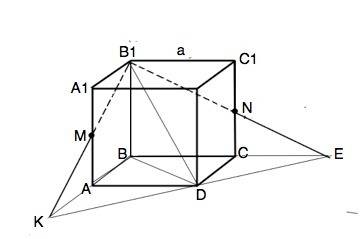
Проведем сечение через В1МN. Оно пересекает плоскость, содержащую грань ABCD, в точках К - на продолжении АВ, и Е - на продолжении ВС.
∆ КВЕ - проекция ∆ КВ1Е на плоскость, содержащую основание куба.
АМ=МА1; CN=NC1 ( дано)
АМ - средняя линия ∆ КВВ1. ⇒ ВК=2а
CN- средняя линия ∆ ВСВ1 ,⇒ ВЕ=2а.
∆КВЕ - равнобедренный прямоугольный. Углы при КЕ=45°
КЕ=ВЕ:sin45°=2a√2
По свойству медианы прямоугольного треугольника медиана (высота, биссектриса) ∆ КВЕ=2a√2:2=a√2
Диагональ ВD квадрата АВСD=а√2
Медиана ∆ КВЕ совпадает с ВD.
Следовательно, плоскость MB1N проходит через вершину D куба.
* * *
Формула диагонали куба а√3. Можно доказать, что медиана ∆ КВ1Е равна а√3 и поэтому совпадает с диагональю куба В1D.
∠CDE составляет одну часть, ∠ADE - 8 таких частей, всего 9 частей.
∠CDE = 90° : 9 = 10°
Сумма острых углов прямоугольного треугольника 90°, тогда из ΔCDE:
∠DCE = 90° - ∠CDE = 90° - 10° = 80°
Диагонали прямоугольника равны и точкой пересечения делятся пополам, тогда ΔCOD равнобедренный (CO = OD), значит углы при его основании равны:
∠OCD = ∠ODC = 80°.
В ΔOCD находим третий угол:
∠COD = 180° - (∠OCD + ∠ODC) = 180° - 160° = 20° - угол между диагоналями.
Объяснение:
Подпишись на меня в ютубе мой канал. LIXORADKA 43. Буду тебя там ждать)