а) боковая сторона равна 4√3 см;
б) медиана, проведённая к основанию, равна 2√3 см;
в) медиана, проведённая к боковой стороне, равна 2√21 см.
Объяснение:
Дано:
ΔАВС:
АВ = ВС - боковые стороны
АС = 12 см - основание
∠А = ∠С = 30° - углы при основании
Найти:
а) АВ - боковую сторону
б) ВМ - медиану, проведённую к основанию
в) АК - медиану, проведённую к боковой стороне
а)
В равнобедренном треугольнике медиана, проведённая к основанию, делит основание пополам, то есть
АМ = СМ =0,5АС = 6 см;
и является высотой, поэтому ΔАВМ - прямоугольный с углом
∠ВМА = 90°.
Тогда
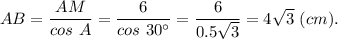
и
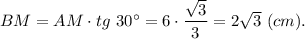
в)
В ΔАВС: ∠В = 180° - 2 · 30° = 120°
Рассмотрим ΔАВК.
АВ = 4√3 см; ВК = 0,5 ВС = 2√3 см; ∠В = 120°.
По теореме косинусов найдём ВК
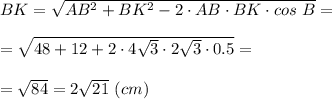
1
Объяснение:
Для решения данной задачи примем катеты за неизвестные. Пусть они равны a и b соответственно. Тогда согласно условиям задачи составим систему уравнений и решим ее, вычтя из первого уравнения второе:
система выражений a в степени 2 плюс b в степени 2 =49,(a минус 4) в степени 2 плюс b в степени 2 =25 конец системы . равносильно система выражений a в степени 2 плюс b в степени 2 =49, 8a=40 конец системы . \underset{b больше 0}{\mathop{ равносильно }} система выражений a=5,b=2 корень из 6 . конец системы .
Таким образом, первоначально горка была высотой 5 м и длиной 2 корень из 6 \approx 4,9 м. После уменьшения горки, ее параметры стали равны 1 м и 4,9 м соответственно.