решение
первая
сумма всег углов тр-ка равна 180 градусов, поэтому разделим 180 пропорционально числам 2,3,4.
1) 180 : (2+3+4) =20 градусов приходится на одну часть
2) 20*2 =40 градусов первый угол
3) 20*3 =60 градусов -второй угол
4) 20*4 =80 градусов третий угол
вторая
1) угол между касательной ас и хордой ав равен половине дуги ав, то есть дуга ав содержит 75*2 =150 градусов
2) центральный угол аов измеряется дугой ав и равен 150 градусов
ответ < аов =150 градусов
третья
треугольники равны по стороне ас ( общая сторона) и двум углам, так как
1) < вас = < асв ( в равнобедренном тр-ке углы при основании равны)
2) < дас =< асе ( по свойству биссектрисы, она делит угол пополам)
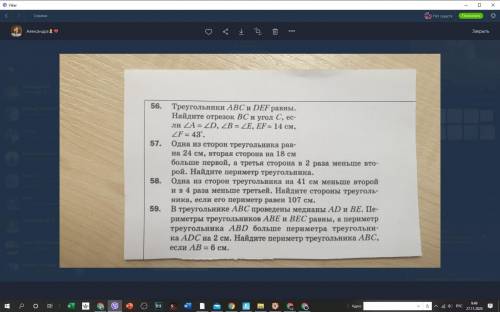
56: ∠C = 43°; ВС = 14
57: 87
58: 11, 52, 44
59: 16
Объяснение:
56: По условию, треугольники равны. В равных треугольниках все соответственные элементы равны. Т.к. ∠А = ∠D, а ∠В = ∠Е, то ∠С = ∠F = 43°. Все равные между собой углы соответственны ⇒ ВС соответствует ЕF ⇒ ВС = ЕF = 14.
57: Назовем стороны треугольника х, х + 18, (х + 18) : 2. Сторона х это та сторона, которая по условию рана 24. Значит, х + 18 = 24 + 18 = 42, а (х + 18) : 2 = 42 : 2 = 21. Периметр треугольника равен сумме его сторон ⇒ Р = 24 + 42 + 21 = 87.
58: Назовем стороны треугольника х, х + 41 и 4х соответственно. По условию периметр равен 107. Составим уравнение: 4х + х + х + 41 = 107. Решим его: 6х = 107 - 41 ⇒ 6х = 66 ⇒ х = 11. Таким образом, х + 41 = 52, 4х = 44. Стороны равны 11, 52, 44
59: Рассмотрим ΔАВЕ и ΔВЕС. ВЕ - общая сторона. АЕ = ЕС по св-ву медианы. Т.к. периметры ΔАВЕ и ΔВЕС равны, а ВЕ общая и АЕ = ЕС, то АВ = ВС. ΔАВЕ = ΔВЕС по трем сторонам. В равных треугольниках все соответственные элементы равны. Также и АВ = ВС = 6. Периметр ΔАВD > периметра ΔАDC на 2. Периметр ΔАВD = АВ + ВD + DА. Периметр ΔАDС = АВ + ВD + DА - 2 ⇒ AD + DC + AC. Т.к. ВD общая, а по св-ву медианы ВD = DС, то АС = АВ - 2 = 4. Периметр ΔАВС = 6 + 6 + 4 = 16