5x - 2y -1 =0; 2x +y -3 = 0; x - 2,7y - 7,1 =0.
Объяснение:
Пусть дан треугольник АВС с вершиной в точке А(1;2).
Эта вершина не принадлежит ни одной из данных нам высот (проверяется путем подстановки координат точки А в оба уравнения.
Уравнения высот можно записать в виде уравнений с угловым коэффициентом:
y = -(2/5)*x - 4/5 (1), где k=-(2/5) и y = (1/2)*x - 5/2 (2), где k= (1/2).
Уравнения сторон АВ и АС треугольника, это уравнения прямых, перпендикулярных данным нам высотам, проходящих через точку А.
Условие перпендикулярности прямых: k1 = -1/k .
Уравнение прямой, проходящей через точку А(xa;ya), перпендикулярно прямой y = kx +b определяется по формуле:
y - ya = -(1/k)*(x-xa). В нашем случае уравнение одной из сторон треугольника будет: y -2 = -(-5/2)*(x - 1) => 5x - 2y -1 =0 (3).
Уравнение второй стороны: y -2 = -(2/1)*(x-1) => 2x +y -3 = 0. (4).
Теперь найдем координаты вершин В и С. Для этого решим системы двух уравнений: (1), (4) и (2), (3):
2x+5y+4=0 и 2x +y -3 = 0 => y = -1,75; x = 2,375. => B(2,375;-1,75)
x-2y-5 = 0 и 5x - 2y -1 =0 => x = -1; y = -3. => C(-1;-3).
Имея координаты точек В и С, напишем уравнение прямой, проходящей через эти точки (третья сторона треугольника) по формуле:
(x-xb)/(xc-xb) = (y-yb)/(yc-yb) => (x-2,375)/(-1-2,375) = (y+1,75)/(-3+1,75) =>
x - 2,7y - 7,1 =0 это уравнение третьей стороны треугольника.
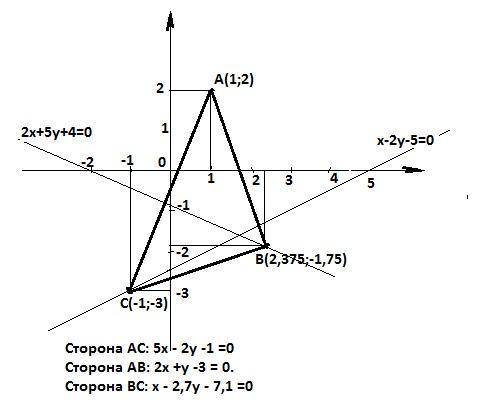
P.S. Для наглядности приложен рисунок. Проверить решение можно, подставляя в уравнения сторон координаты вершин, принадлежащих этим сторонам.
В получившемся прямоугольном (т.к. BD-высота) треугольник ЕВD нам известна гипотенуза ВЕ=13см и противолежащий катет ВD=12см. Находи угол ВЕD: sinBED=12/13=0,923076, arcsinBED=67,38 градусов. Находим отрезок ED через cosBED=х/13. х=cosBED*13=cos(67,38)*13=5 см.
Рассмотрим прямоугольный треугольник АВD. Сторона АD=АЕ+ЕD. Т.к. медиана ВЕ делит основание АС=60 см пополам, то отрезок АЕ=60/2=30 см.
АD=30+5=35 см. Согласно теореме Пифагора в прямоугольном треугольнике АВD квадрат гипотенузы АВ равен сумме квадратов катетов ВD и АD, т.е.
АВ
АВ=
АВ=
АВ=