Соединение средин сторон треугольника называется средней линией треугольника. Она расположена параллельно третьей стороне, а длина ее равна половине длины этой стороны. Поэтому можно утверждать, что и стороны меньшего треугольника так же будут относится как 4:3:5.
Так как периметр треугольника, образованного средними линиями равен 3,6 дм, а стороны относятся как 4:3:5, то выразим это следующим образом (Для удобства вычисления переведем все величины в сантиметры 1 дм = 10 см):
4х – длина отрезка АВ;
3х – длина отрезка ВС;
5х – длина отрезка АС;
4х + 3х + 5х = 36;
12х = 36;
х = 36 / 12 = 3;
АВ = 4 · 3 = 12 см;
ВС = 3 · 3 = 9 см;
АС = 5 · 3 = 15 см.
ответ: стороны треугольника, образованного средними линиями равны 12 см = 1,2 дм, 9 см = 0,9 дм, 15 см = 1,5 дм.
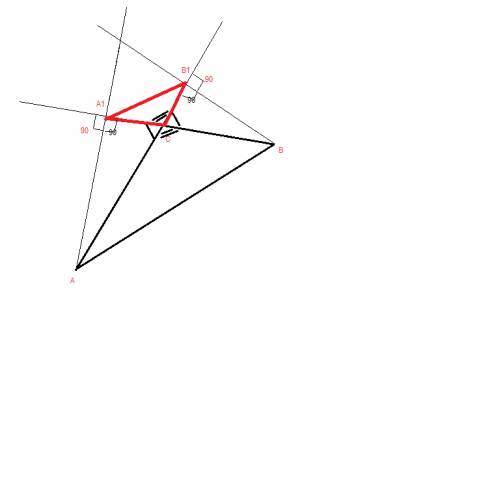
Доказать подобие треугольников А1СВ1 и АВС.
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
ab=bc/sinA
2/0,4=20/4=5
ответ 5