" Основой прямой призмы является равнобедренный треугольник с углом a при основании и радиусом вписанной окружности r. Диагональ боковой грани, проходящей через основание равнобедренного треугольника, наклонена к плоскости основания под углом y . Отметьте, какие из приведенных четырех утверждений правильные
1. Плоскость, проходящая через боковое ребро призмы и уентр круга, вписанного в основание, делит двугранный угол при боковом ребре призмы пополам
2. Боковое ребро призмы равна 2r*ctg*a/2*tgy
3. Одна из сторон основания призмы равна r*ctg*a/2
4. Один из двугранных углов при боковом ребре призмы равна a"
Объяснение:
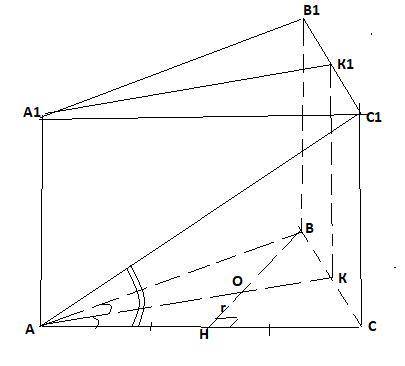
1) Т.к. центр вписанной окружности лежит в точке пересечения биссектрис, то плоскостью, проходящей через боковое ребро призмы и центр круга, вписанного в основание, будет плоскость АКК₁А₁ , где АК, А₁К₁-биссектрисы нижнего и верхнего оснований.
Поэтому 1 утверждение верное.
2) Боковое ребро найдем из ΔАСС₁ -прямоугольного : СС₁=АС*tgy.
АС найдем из ΔАОН :
ΔАВС-равнобедренный. В равнобедренном
треугольнике биссектриса ВН является высотой и
медианой .АК-биссектриса, значит ∠ОАН=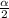
.
АН=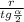
, 2АН=АС=
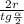=2r*ctg .
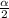Получаем СС₁=2r*ctg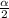 *tgy.
Поэтому 2 утверждение верное.
3) 3 утверждение неверное , т.к. в п 2 найдена сторона основания АС=2r*ctg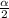 . а боковая сторона будет искаться через косинус или синус ΔАВН.
4)4 утверждение верное . Это двугранный угол , например САА₁В, т.к
АА₁⊥АС и АА₁⊥АВ и ∠ВАС=α
Дано:
АС=7 см;
АВ=25 см;
ВС=24 см.
СО – высота, проведенная к АВ.
Высота, пересекаясь со стороной, к которой проведена, образует прямой угол.
То есть угол ВОС=90° и угол АОС=90°.
Следовательно ∆ВОС – прямоугольный с прямым углом ВОС и ∆АОС – прямоугольный с прямым углом АОС.
Пусть АО=х, тогда ВО=АВ–АО=25–х.
По теореме Пифагора в прямоугольном треугольнике ВОС:
ВС²=ВО²+СО²
СО²=ВС²–ВО²
СО²=24²–(25–х)²
СО²=576–625+50х–х²)
СО²=–х²+50х–49 (Ур 2)
По теореме Пифагора в прямоугольном треугольнике АОС:
АС²=АО²+СО²
СО²=АС²–АО²
СО²=7²–х²
СО²=49–х² (Ур 2)
Тогда можем составить уравнение, объединив Ур 1 и Ур 2, получим:
–х²+50х–49=49–х²
50х=98
х=1,96
Тоесть АО=1,96 см.
Подставим значение АО и известное значение АС в уравнение СО²=АС²–АО², получим:
СО²=49–3,8416
СО²=45,1584
СО=6,72 см.
ответ: 6,72 см.