Объяснение:
1. <ABM=<BAC, <CBF=<ACB как накрест лежащие. Пусть x - 1 часть. Значит <ABM=3х, <ABC=5x, <CBF=2x. Их сумма равна 180гр. Значит 3x+5+2x=180 x=18.
<BAC=3*18=54, <ABC=5*18=90, <ACB=2*18=36
2.
ответ будет 50гр, но я решил через сумму четырехугольника.
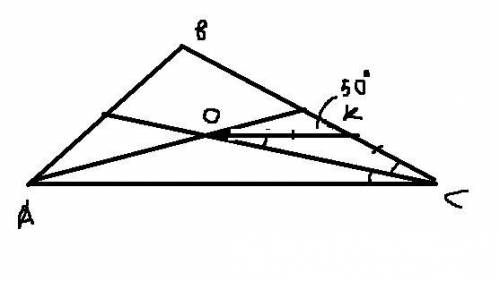
3. Рассмотрим тр-к OKC. В нём OK=KC по условию, значит он равнобедренный и <COK=<OCK. Но при этом он же будет равен <ACO т.к. CO - биссектриса. Отрезки OK и AC будут параллельны, т.к. в них накрест лежащие углы <COK и <ACO равны. (Теорема если при пересечении двух прямых секущей ( в данном случае биссектрисой CO) накрест лежащие углы оказываются равны, то значит, эти прямые параллельны.) Из этого следует, что cоответственные углы <BKO=<ACB=50гр при пересечении секущей BC. Тогда находим <COK=<OCK=1/2*<ACB=25гр
Если нельзя применить теоремы синусов и косинусов, то, скорее всего, можно применить теорему Пифагора.
Пусть высота треугольника АВС из точки А равна Н.
Опустим из основания биссектрисы перпендикуляр h на сторону ВС.
Из подобия треугольников имеем h/H = 4/20 = 1/5,
По Пифагору находим:
Н = √(20² - (5/2)²) = √(400 - (25/4) = √(375/4) = 15√7/2.
Теперь получаем: h = (1/5)*(15√7/2) = 3√7/2.
Длину биссектрисы L тоже определяем по Пифагору.
Проекция её на ВС равна (5/2) + (4/5)*(5/2) = 9/2.
L = √((9/2)² + h²) = √((81/4) + (63/4)) = √(144/4 = √36 = 6.
ответ: длина биссектрисы равна 6.