Центр окружности, проходящей через точки А и В, равноудален от этих точек. А все точки, равноудаленные от концов отрезка АВ, лежат на серединном перпендикуляре к нему. Т.е. центр окружности, проходящей через точки А и В, лежит на серединном перпендикуляре к отрезку АВ.
Наименьшее расстояние от точек А и В до прямой а - длина перпендикуляра, проведенного к а, т.е. R = HA = HB = 1 см. Если же центр окружности не совпадает с точкой Н, то радиус будет больше, чем НА (гипотенуза ОА в прямоугольном треугольнике АОН больше катета НА).
A1.
Sшестиугольника =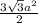 
ответ: 4
A2.
Правильный четырёхугольник - это квадрат. Так как он вписан в окружность, то диаметр окружности будет равен диагонали квадрата. Диагонали квадрата пересекаются в центре и делят его на 4 одинаковых прямоугольных равнобедренных треугольника с бок. сторонами = R ⇒ S квадрата равна площади четырех треугольников:
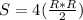
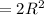
ответ: 1
A3.
Правильный шестиугольник состоит из 6 равносторонних треугольников, стороны которых равны a, а высоты равны радиусу R. Найдем, чему равны стороны через высоту (радиус):
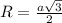
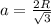
Площадь одного треугольника будет равна:
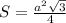
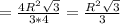
Площадь шестиугольника:
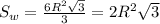
ответ: 2
B1.
Пусть вписанный треугольник - ΔABC, сторона = 
; описанный - ΔA₁B₁C₁, сторона -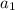 
Для ΔA₁B₁C₁ радиус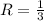 
высоты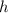 
⇒
⇒ 
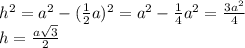
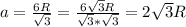
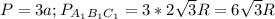
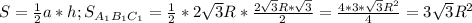
Для ΔABC радиус R =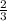 
высоты :
⇒
⇒ 
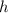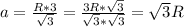
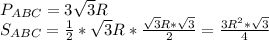
Найдем соотношение периметров и площадей:
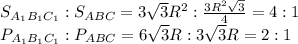
27.б) Sabc1d1 = 10см²
27.д) стороны равны 9 см и 8 см.
Объяснение:
27.б) AD1 = 5см (треугольник ADD1 - пифагоров).
Сечение - прямоугольник АВС1D1.
Площадь равна АВ·AD1 = 2·5 = 10 см².
27. д) Sabcd = a·b = 72 cм² => b = 72/a. (1)
BD = √(B1D² - BB1²) = √(17² - 12²) = √145. (из треугольникаBB1D по Пифагору).
BD² = a² +b² (из треугольника АВD по Пифагору). Тогда a² +b² = 145 (2). Подставим (1) в (2):
a² + (72/a)² = 145. и заменим a² на х. =>
х² - 145х + 5184 = 0. Решаем квадратное уравнение и получаем х = (145±17)/2 => х1 = 81 и х2 = 64. Тогда стороны основания равны √81 = 9см и √64 = 8см.